El método de Gauss- Jordan

1. El método de Gauss – Jordan también es denominado “de eliminación de Gauss – Jordan”. Es una metodología para resolver sistemas lineales de ecuaciones con n variables, la idea es escribir el sistema en matrices y sus inversas.


2. Para la solución de sistemas aplicando este método, se deben escribir los coeficientes de las variables de las ecuaciones lineales en su notación matricial:
   
   

   




3. Entonces, se lleva a la forma de matriz aumentada:

   



4. Hecho esto, se convierte dicha matriz en una matriz identidad, la cual es de la forma:
   
   

   

   
   Esto se logra aplicando operaciones entre filas y columnas.
   
   Obsérvese que en dicha matriz identidad no aparecen los términos independientes, esto se debe a que al reducirla, la igualdad será:
   
   
   d1 = x
   d2 = y
   d3 = z

Ejemplo:

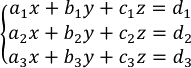
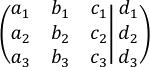
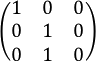
Sea el sistema de ecuaciones:

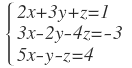
a. Escrito en forma matricial es:

b. Se procede a operar con las distintas filas y columnas de la matriz para transformarla en su matriz identidad:

c. Primero transfórmese el 2 de la 1ª fila de la matriz original en el 1 de la 1ª fila de la matriz identidad multiplicando por el inverso de 2, es decir ½.

d. Obténganse los dos ceros de la primera columna de la matriz identidad, para lograr esto, multiplique la fila 1 por -3 y por -5 y súmense todos estos productos de la fila 1 a la 2ª y 3ª fila respectivamente.

e. El siguiente paso es obtener el 1 de la 2ª fila de la matriz identidad, y procedemos de igual forma que antes, es decir multiplicando toda la fila por el inverso, en este caso -13/2, cuyo inverso es -2/13. Además la tercera fila, si tiene todos los elementos con el mismo denominador, entonces pueden eliminarse multiplicando todos estos por 2 (el denominador); lo que es útil para facilitar los cálculos.

f. Ahora debe obtenerse el 0 que se ubica en la 3ª fila, 2ª columna, para esto se busca el opuesto del número que se ubica en la 3ª fila, 2ª y 1ª fila 2ª columna de la matriz:

g. En éstas condiciones comienza a aparecerse la matriz identidad.

h. Finalmente se obtiene los dos ceros de la tercera columna de la matriz identidad, para lograr esto, se busca el opuesto de 96/13 y se multiplica la 3ª fila y por los opuestos de la 2ª y 1ª fila para sumar y reducirlos a cero, es decir:

i. El último paso es convertir en 0 el 3/2 de la 1ª fila, obsérvese la operación efectuada:

j. Luego la solución es: x= 1, y= -1, z= 2.