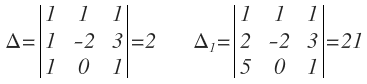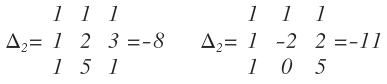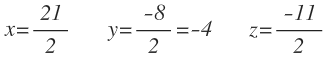La regla de Cramer se aplica a sistemas que cumplan las siguientes condiciones:
El número de ecuaciones es igual al número de incógnitas.
El determinante de la matriz de los coeficientes es distinto de cero.
Así, los sistemas de ecuaciones que cumplen las condiciones se denominan sistemas de Cramer.
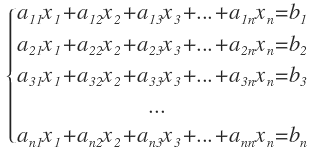
Sea Δ el determinante de los de coeficientes:

Y sean: Δ 1, Δ 2 , Δ 3 ... , Δ n
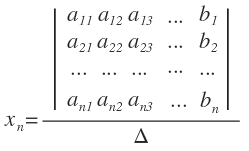
Los determinantes obtenidos del cociente por la sustitución de los coeficientes del 2º miembro del sistema (los términos independientes) en la 1ª columna, en la 2ª columna, en la 3ª columna y en la enésima columna respectivamente, generan la solución única del sistema.
El sistema de Cramer tiene una sola solución y está dada por las siguientes expresiones:
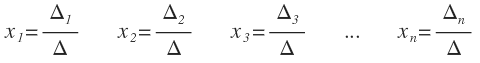



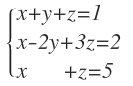
Aplicando el método de Sarrus o cualquiera de los vistos: