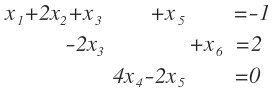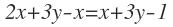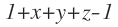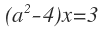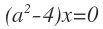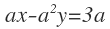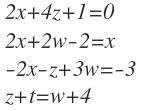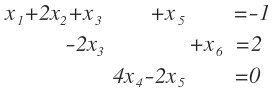Ejercicios de representación matricial
1. Considere las siguientes ecuaciones:
- Diga si cada ecuación es lineal o no lineal; si es lineal determine si es homogénea o no homogénea.
- Para cada ecuación, escriba sus coeficientes, su término constante y su ecuación homogénea asociado.
- Para cada ecuación lineal ordene sus variables y diga cuál es la variable delantera y cuáles son las variables libres.
2. Encuentre todos los valores, tales que cada una de las siguientes ecuaciones tenga:
- Exactamente una ecuación.
- Soluciones infinitas.
- Ninguna solución.
3. Remplace el sistema lineal en la forma canónica, es decir en forma matricial:
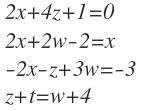
4. Determine:
- Determine coeficientes.
- La matriz aumentada.
- El sistema homogéneo asociado.
5. Aplique la sustitución hacia atrás para resolver el sistema: