MÉTODO DE GAUSS

Consiste en transformar la matriz en otra equivalente por filas así:

1. Formar una matriz de orden n x 2n tal que las n primeras columnas son la matriz A y las otras n las de la matriz identidad de orden n.
2. Mediante las transformaciones de las filas de una matriz, convertir la matriz anterior en otra que tenga en las n primeras columnas la matriz identidad y en las n últimas otra matriz que precisamente será A-1.

Ejemplo 1

Hallar A-1, si a es invertible.

Ejemplo 2

Hallar la inversa de A.

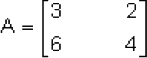
Solución:

Las primeras dos columnas de la última matriz forman una matriz reducida diferente de I. Por tanto A no es invertible.

Ejemplo 3

Hallar la inversa de:

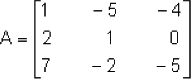
Solución:

Se tiene que:

Comprobando, se tiene: como A·A-1 = I, entonces:

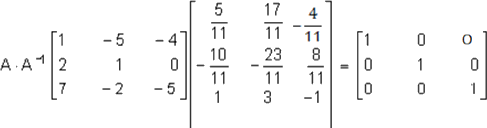
Si la matriz a es de orden 2 y se trata de hallar su inversa, un sistema de ecuaciones resuelve el problema:

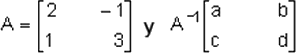
Se cumple que:

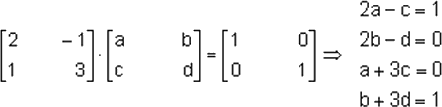
Agrupando:

Y resolviendo cada sistema donde:

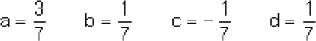
De tal manera que:

Ejercicios

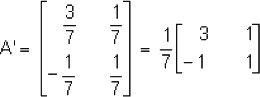
1. Determine si las matrices siguientes son invertibles:

2. Determine la inversa de las siguientes matrices, sabiendo que:

3. Determine A-1; B-1; C-1 si:

4. Resuelva A·X = B si: