

Verificar que:

Para de f si A·B = B·A = I entonces B es la inversa de A, entonces:
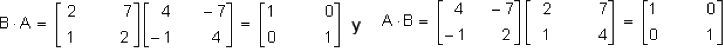
En el caso de las matrices 2 x 2 se puede determinar exactamente cuáles son invertibles y citar una fórmula explícita de la inversa. Esto es más difícil de predecir para tamaños mayores de 2 x 2.
Sea:
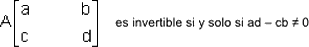
en cuyo caso:
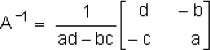
Determinar si A es invertible y calcular A-1
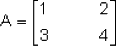
Solución:
1·4 - 2·3 = 4 – 6 = - 2 -2 ≠ 0
Por consiguiente A tiene inversión:
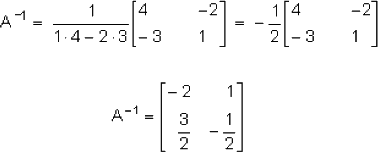
Mostrar que:

Solución:
1·0 - 0·0 = 0 – 0 = 0 por lo tanto no es invertible. Si la matriz A, n x n puede invertirse, el sistema Ax = B tiene exactamente una solución para cada vector B. Esta solución única es:
X = A-1B
Aplíquese la inversión matricial, para resolver el sistema.
x– 4y = 2
x– 3y = 1
Solución:
La ecuación matricial del sistema es:
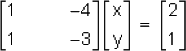
Entonces:
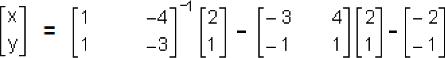
Por consiguiente:
x = - 2
Y = - 1
Una matriz A posee inversa si y solamente si es cuadrada, y el producto de su inversa por A es la matriz idéntica. Existen diferentes métodos para hallar la inversa.
1. Hallar la matriz inversa en caso de ser invertible, en caso contrario escribase porque no es invertible.
2. Resuelva Ax = B, si:
3. Si la matriz de coeficientes del sistema es invertible, resuélvase el sistema, utilizando la inversa, si no es así, resuélvase el sistema por el método de reducción.