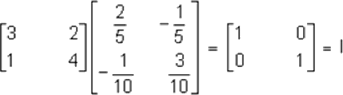Si A, B y C tienen el mismo orden, entonces las propiedades siguientes se cumplen para la suma de matrices.
Sean:
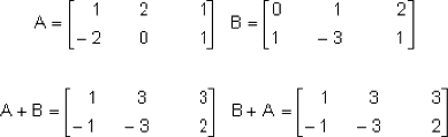
Por lo tanto: A+B = B+A
Sea:
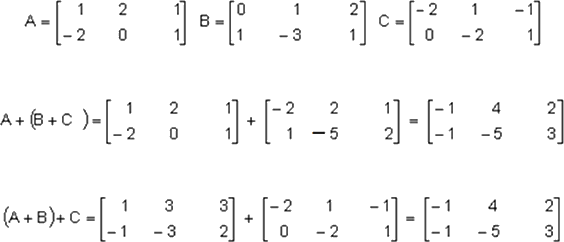
Por tanto: A+(B+C) = (A+B)+C
Sea:

Por tanto: C+0 = C
Si:
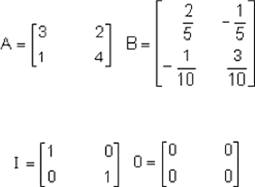
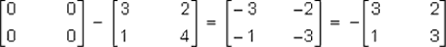
Es decir: O-A=-A
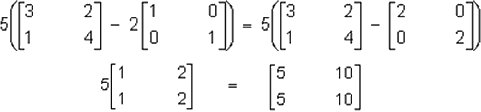
La multiplicación de matrices tiene dos propiedades:
Ejemplo:
Si:
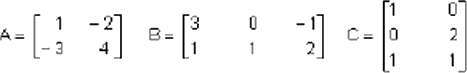
Tenemos que: A(BC) = (AB)C
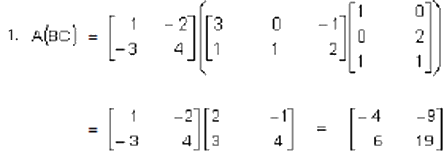
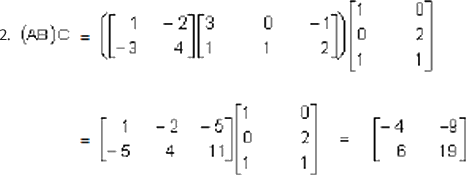
Nota: El resultado en 1 es igual a 2, por lo tanto A(BC) = (AB)C.
Ejemplo 1:
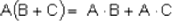

Ejemplo 2:
Si:
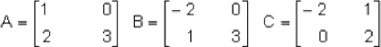
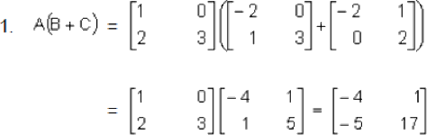
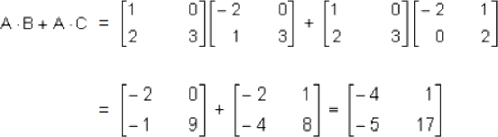
Nótese que los resultados I y II son iguales porlo tanto A(B+C) = A*B + A*C
Ejemplo 3:
(A+B)*C = A*C + B*C
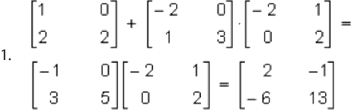
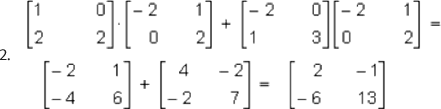
Como los resultados de 1 y 2 son iguales, entonces: (A+B)C = A*C + B*C.
Si A*B = 1, entonces B es la inversa multiplicativa de A.