

Buscando formas para describir situaciones en matemáticas y economía, llegamos al estudio de arreglos rectangulares de números, por ejemplo, considérese el sistema de ecuaciones lineales:
(K1+K2)A=K1+K2A
que caracteriza a estos sistemas son los coeficientes numéricos en las ecuaciones junto con sus posiciones relativas. Por esta razón, el sistema puede ser descrito por el arreglo rectangular:
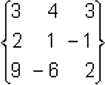
Que es llamado matriz, considérese a tales arreglos rectangulares como objetos de si mismos y, se acostumbra cerrarlos entre corchetes normales { } y/o rectos [ ]. También es común que se utilicen paréntesis ( ). En la representación simbólica de matrices, se usa letras mayúsculas como A, B, C.
En Economía y Administración con frecuencia es conveniente utilizar matrices en la formulación de problemas y para exhibir datos. Por ejemplo, un fabricante de los productos A, B, y C podría representar las unidades de mano de obra y material involucrados en una semana de producción de estos artículos así:
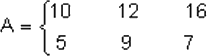
| Producto | |||
| A | B | C | |
| Mano de obra | 10 | 12 | 16 |
| Material | 5 | 9 | 7 |
Los renglones de una matriz están numerados de manera consecutiva de arriba hacia abajo, y las columnas están numeradas de manera consecutiva de izquierda a derecha. Para organizar la matriz se tiene A=:
| A | B | C | |
| Renglón 1 | 10 | 12 | 16 |
| Renglón 2 | 5 | 9 | 7 |
Ya que A tiene dos renglones y tres columnas, se dice que A tiene orden o tamaño 2x3, donde el número de renglones se especifica primero. Obsérvese el orden de las matrices B y C.
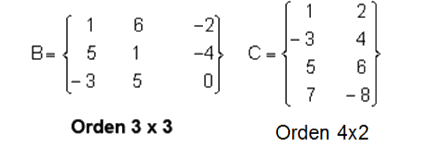
Los componentes de una matriz son llamados entradas o elementos. Para denotar entradas arbitrarias de una matriz por ejemplo de una de tamaño 2x3, existen dos métodos comunes. Primero, se puede utilizar letras diferentes:
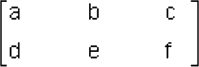
Segundo, una sola letra se puede usar, suponga aij junto con doble subíndice i y j apropiado para indicar su posición.
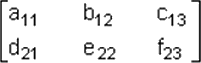
Un arreglo rectangular de números que consiste en unos renglones y en columnas.
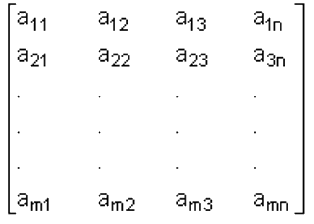
Es llamado matriz mxn o matriz de orden mxn. Para la entrada ai se dice que i es el subíndice del renglón y i el subíndice de la columna.
El número de entradas en una matriz de m x n es mn. Por brevedad una matriz de m x n puede ser denotada por el símbolo a:j o de manera más sencilla aij donde el orden se entiende que es el apropiado para el contexto dado. Esta notación solo indica qué tipo de símbolos son utilizados para denotar la entrada general.
Una matriz que tiene exactamente un renglón se nota con a1j. Una matriz que consiste en una sola columna se nota con aj1, tal como la matriz de orden 5 x 1 [a51]
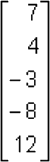
Es llamada matriz columna, o vector columna.
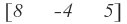 tiene orden 1x3.
tiene orden 1x3.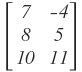 tiene orden 3x2.
tiene orden 3x2.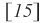 tiene orden 1x1.
tiene orden 1x1.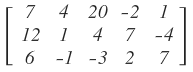 tiene orden 3x5.
tiene orden 3x5.| 1. |  |
| 2. | 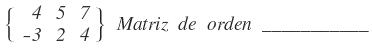 |
Construir una matriz columna de tres entradas, tal que a21= 6y a11= 0 en los otros casos.
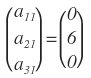
Si A = [aij] tiene orden 3 x 4 y aj = i+j encontramos A:
Solución:En este caso i = 1, 2, 3 y j = 1, 2, 3 ,4 y A tiene (3) (4) = 12 entradas. Ya que aij = aij = i + j.
Se tiene:
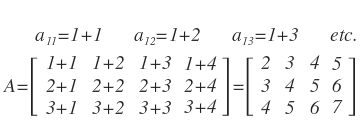
Construir la matriz de I de 3 x 3 dado que a11 = a33 = 1 y aij=0 en cualquier otro caso.
Solución: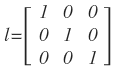
[1]Ardila Duarte, G. (2013). Ejemplos y ejercicios de orden y construcción de una matriz. Bogotá.