EJEMPLOS RESUELTOS

Multiplicación por una matriz escalar

Sí A es una matriz m x n, y Q y R son matrices escalares m x m y m x n, respectivamente (con el escalar c en sus diagonales principales), pueden combinarse las propiedad 4 y 5 del teorema 2 para calcular.

QA=(cl_m) A=c(I_mA)=cA

Igualmente, AR = cA por consiguiente, QA=AR=cA

En otras palabras, la multiplicación por una matriz escalar es igual que la multiplicación por un escalar. Además, la suma, diferencia y producto de las matrices escalares que poseen el mismo tamaño, dan como resultado una matriz escalar.

Aplicación a la economía

Con frecuencia, los economistas estudian las condiciones para los equilibrios de mercados; es decir, las condiciones bajo las que se relacionan los precios de diversos artículos.

Por ejemplo, examinando los mercados relacionados de bolígrafos y lápices. Sean P₁ y P_b los precios en dólares de un lápiz o un bolígrafo, respectivamente. Algunas condiciones del mercado obligan a que los dos precios satisfagan la relación P₁ + P_b=1.5, mientras que otras circunstancias requieren de la relación P₁ - P_b=0.5. El precio de equilibrio para cada mercado es aquel que cumple ambas condiciones.

Ésta es la solución del sistema de las dos ecuaciones.
Así, los precios de equilibrio son P₁ = 1 y P_b =0.5.

Ejemplo: equilibrio en mercados relacionados.

Las condiciones de equilibrio entre tres mercados relacionados (carne de pollo, de cerdo y de res) se expresan como sigue:

5P_p - P_c - 2P_r = 1

-2P_p + 6P_c - 3P_r = 3

-2P_p - P_c + 4P_r = 10

Calcule el precio de equilibrio en dólares para cada mercado.

Solución

El sistema AP = B, con:

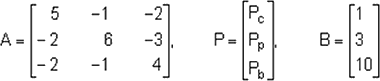
Puede resolverse invirtiendo A, Si empleamos el algoritmo de inversión de matrices se obtiene:

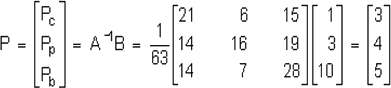
Por consiguiente, los precios de equilibrio son $3 para la carne de pollo, $4 para la de cerdo y $5 para la de res.

La inversa con sistemas algebraicos computacionales Excel:

Se escribe la matriz, en cada celda de Excel se escribe una entrada de la matriz.
Se ubica en una celda vacía, que no posea elementos de la matriz que escribió en la hoja electrónica.
Se oprime clic izquierdo en f_x, ubicado en el extremo izquierdo superior de la hoja electrónica.
Se oprime clic en usadas recientemente, para buscar todo.
Se busca MINVERSA, en el menú.
Se señala la matriz que escribió.
Dar clic en aceptar.
Se sostiene oprimido el mouse, hasta sombrear tantas celdas vacías como el tamaño de la matriz a la que se le calculará la inversa.
Dar clic al lado de f_x.
Oprimir ctrl+Shift+enter
Listo, obtiene la inversa de la matriz en Excel.

Ejercicios:

Aplique el teorema 4 para determinar las inversas de las matrices siguientes y use Excel.
Utilice el teorema 4 para explicar por qué las matrices siguientes no son invertibles.

Economía: modelos de entrada y salida de Leontief

Suponga una economía formada por n industrias, cada una produciendo sólo un artículo necesario para los demás y posiblemente para sí misma.
Por ejemplo, suponga que se tuviera carbón, acero y automóviles y que su interrelación estuviera descrita por una matriz de 3 x 3 como sigue: si Cij es el valor en dólares del i-ésimo artículo necesario para producir la cantidad de j-ésimo producto valuada en 1 dólar, así se necesitan 0.30 dólares de carbón para producir 1 dólar de acero. El valor 0.30 es el elemento (1,2) de la matriz.

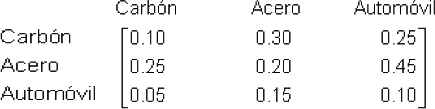
Según esta matriz, también se necesitan 0.45 dólares de acero para producir la parte de un automóvil valuada en 1 dólar. Obsérvese que el automóvil es el mayor consumidor de acero y el acero es el mayor consumidor de carbón. La industria del acero depende más de la automovilística para sobrevivir.

Éste ejemplo de matriz de entrada y salida, o de consumo, que describe la interdependencia de los sectores económicos. Los elementos de esa matriz son positivos y menores que 1. Además, la suma de los elementos de cada columna debe ser menor que 1 si cada sector debe producir más de lo que consume. Las matrices de consumo fueron introducidas y estudiadas por Wassily W. Leontief, economista de Harvard, en la década de los treinta y premio Nobel de Economía en 2004.

Suponga que n sectores económicos se interrelacionan en una forma descrita por una matriz de consumo C=[c_ij]. Sea x_i la cantidad total de producción necesaria para que el i-ésimo sector satisfaga las demandas de todos los demás. Entonces, c_ijx_ij es la cantidad necesaria del artículo i para producirxjunidades del artículo. Como la producción total de la industria i es igual a la suma de las demandas de todos los sectores.

X_i=C₁₁X₁+....+C_1nX_n

...

X_n=C_n1X₁+....+C_nnX_n

Sí X es el vector cuyos componentes son x1,…xn estas relaciones pueden expresarse con la ecuación matricial:

X=Cx

Hasta ahora sólo hemos considerado demanda de artículos por parte de los sectores económicos productivos. Este caso se llama modelo cerrado de Leontief. En realidad, también hay demanda por parte de sectores no productivos, como los consumidores, los gobiernos etc.

En general, una matriz C se llama Productiva si existe (I-C)-1y tiene elementos no negativos.

Por ejemplo, el gobierno puede tener demanda de carbón, acero y automóviles. Todos los sectores no productivos forman el sector abierto. Suponga que di es la demanda del sector abierto, hacia el i-ésimo sector productivo.
Entonces, x_i=c₁₁x₁+…+ c_1nx_n+d_i. Si d es el vector con componentes d₁,…,d_n, no negativos, entonces:

X=Cx+d

Esta ecuación matricial describe un modelo abierto de Leontief, y toma en cuenta el sector abierto; x es el vector salida y d es el vector demanda. Por lo general, a los economistas les interesa calcular el vector de salida x dado el vector demanda d. Esto se puede hacer despejando a x como sigue:

X=Cx+d→ (I-C)x = d→X=(I-C)^-1

Siempre que la matriz I-C sea invertible. Si además (I-C)^-1 tiene elementos no negativos, los elementos de x son no negativos, y por consiguiente se pueden aceptar como valores de producción. En general, una matriz C se llama Productiva si existe (I-C)^-1 y tiene elementos no negativos.