

El menor ij denotado por Mij o |Aij|, es el determinante que resulta de suprimir la fila i y la columna j en un determinante.
Por ejemplo: Considérese el siguiente determinante:
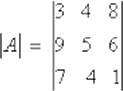
Hállese el menor M11 para esto se elimina la primera fila y la primera columna.
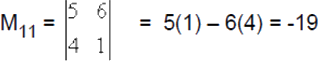
El menor M12 es el determinante que se obtiene después de eliminar la fila 1 y la columna 2 en el determinante es:

El coeficiente ij denotado por cij se define por: Cij=(-1)i+jMij
Por ejemplo:
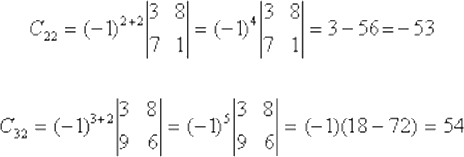
La ley de Sarrus nos permite resolver determinantes de orden tres, el método de cofactores es utilizado para resolver determinantes de cualquier orden. Dado el determinante A de orden cuatro, este determinante se puede resolver por cualquier fila o por cualquier columna utilizando el método de cofactores. Para resolver un determinante por cofactores seleccionamos la fila o columna con el mayor número de ceros.

La matriz está encerrada, entre dos paréntesis, llaves y/o corchetes, en un medio de trabajo y/o real son la base de datos, u organización de información con la que se cuenta a diario, mientras los determinantes están encerrados entre dos barras parecidas a las de valor absoluto, y son una función de la matriz que representa un valor numérico de la misma.
Para calcular un determinante por el método de cofactores, se selecciona el cofactor o coeficiente de la matriz que se ubica a manera de pivote sin incluir la fila y columna que se intersecan en este elemento, para con ellos organizar el determinante a calcular.
Resolver el siguiente determinante:
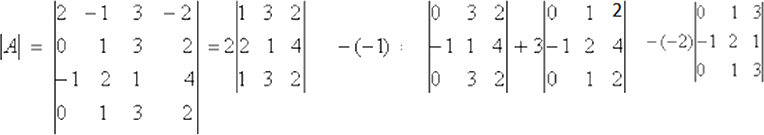
|A|= 2(0)+1(0)+3(0)+2(0)=0
Obsérvese que los determinantes de orden tres tienen dos filas iguales y por propiedades el valor de cada uno es cero.
Hallar el valor determinante:
