A→|A|
nxn número real= Determinente de A
Sí A= |a| es una matriz cuadrada de orden 1, entonces |A| es el determinante.
Sí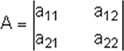 
es una matriz cuadrada de orden 2 entonces: 
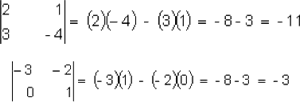
Sea:
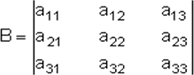
El determinante de B puede escribirse en términos de 2 x 2 así:
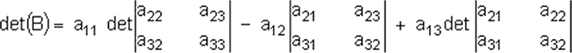
o en la forma:
También, hay un artificio para resolver un determinante de 3 x 3 llamado esquema de Sarrus, que consiste en: agregar las dos primeras columnas a la derecha de B y se forman los productos de los elementos que atraviesan las flechas.
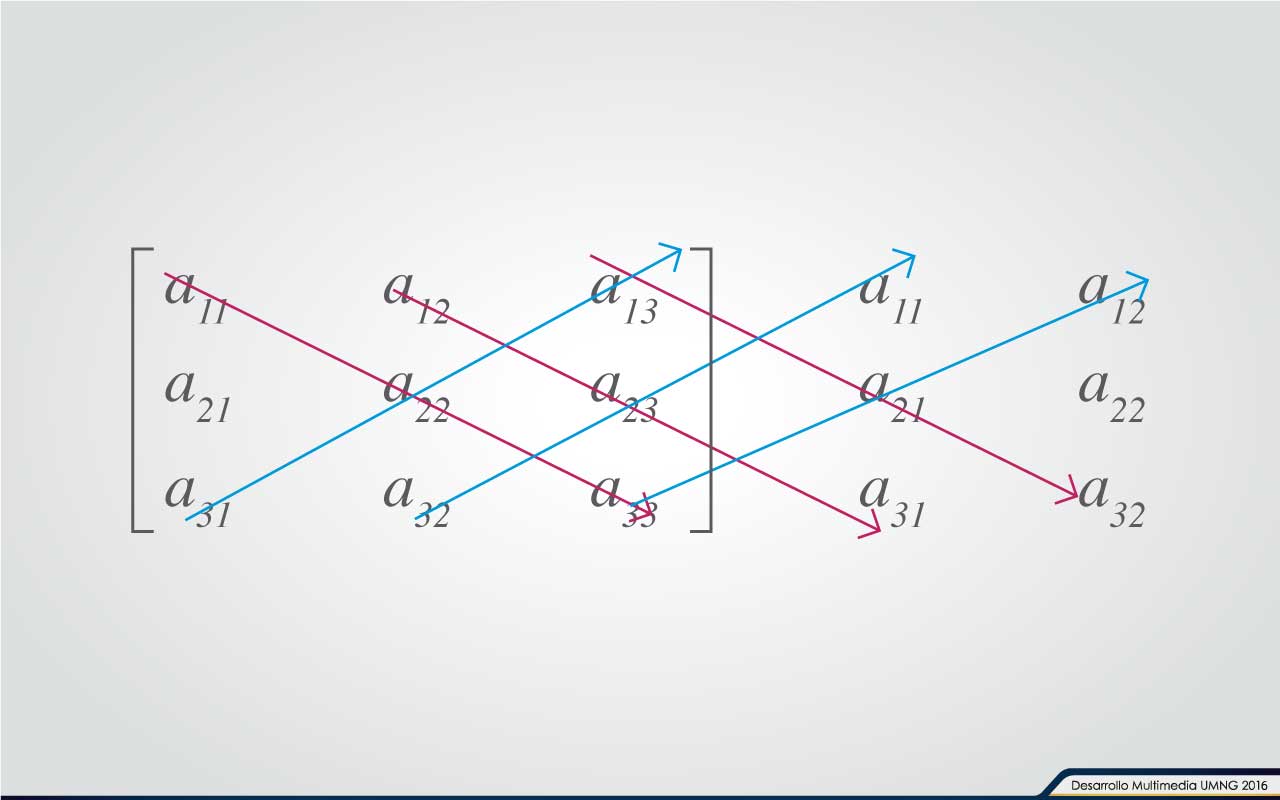
Det(B)= a11*a22*a33+a12*a23*a31+a13*a21*a32-a31*a22*a13-a32*a23*a11-a33*a21*a12
El esquema o Ley de Sarrus no se aplica a los determinantes de 4 x 4, 5 x 5 y a las de más alto orden.
Sea:
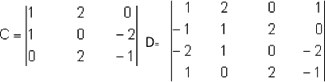
Aplicando la Ley de Sarrus: Det( C)= 1*0*-1+2*-2*0+0*1*2-0*0*0-2*-2*1-1*-1*2=6
Ahora por determinates de 2x2, se obtiene:
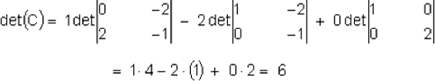
Para hallar el determinante de D, se puede continuar en la misma forma que en los de 2x2 y definir los determinantes de orden n x n en términos de los de (n-1)x(n-1), los cuales se llaman menores.
El menor (i,j) de una matriz A se representa por Mij y es el determinante que se obtiene eliminado el i-ésimo renglón y la i-ésima columna de A. El elemento aij de la matriz es el coeficiente que multiplica la menor Mij, se sugiere tomar la fila i o la columna j que posea más ceros, de ésta forma estos productos dan ceros y es más rápida la operación; a cada coeficiente aij le antecede un signo, que depende del resultado de la suma de i+j, si esta suma es par le antecede un + si esta suma es impar le antecede un menos.
Hállese el determinante de D usando la columna 3:
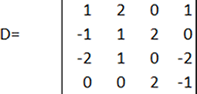
Los elementos de la columna 3 son:
Los elementos de la columna 3 son:
0=a13, como 1+3=4, el signo es +, es decir el coeficiente será:+0
2=a23, como 2+3=5, el signo es -, es decir el coeficiente será: -2
0=a33, como 3+3=6, el signo es +, es decir el coeficiente será:+0
2=a43, como 4+3=7, el signo es -, es decir el coeficiente será: -2
En estas condiciones:
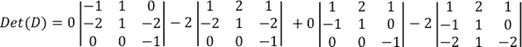
Y el Det(D)=0-2(1*1*-1 + 2*0*0 +1-1*0 - 0*1*1 – 0*0*1 - (-1)*-1*2 + 0 -2(1*1*-2 + 2*0*-2+ 1*-1*1 - (-2)*1*1 - 1*0*1 - (-2)*-1*2)
Det(D)= 0- 2(-1+0+0-0-2-2) -2(-2 +0 -1 +2 -0 -4)
Luego, Det (D)= 10+10=20