

Calcular:
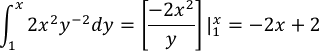
Calcular:
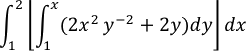
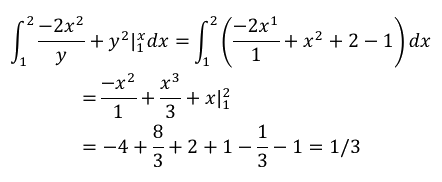
Los límites interiores de integración pueden ser variables respecto de la variable exterior de integración. Por el contrario, los límites exteriores de integración han de ser constantes con respecto a las dos variables de integración. Una vez efectuada la integración interior, se llega a una integral definida ordinaria y la segunda integración produce ya un número real.
Los límites de integración de una integral iterada identifican dos intervalos para las variables. Así, en el ejemplo 1 los límites exteriores indican que x está en el intervalo 1≤x≤2 y los interiores indican que y está en el intervalo 1≤y≤x.
Conjuntamente, esos dos intervalos determinan la región de integración R de la integración iterada.

Puesto que una integral iterada no es sino un caso especial de integral definida, en el que el integrando es a su vez una integral, se puede utilizar las propiedades de la integrales definidas al evaluar integrales iteradas.
En el resto de la sección se contempla desde una perspectiva nueva, el viejo problema de calcular el área de una región en el plano. Considérese la región plana R acotada por a≤x≤b y g(x1)≤y≤g(x2). Su área viene dada por la integral definida.
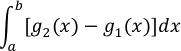
Gracias al teorema fundamental del cálculo, se puede reescribir el integrando g(x1)-g(x2) como una integral definida. En concreto, si se considera que x está fija y se hace variar y desde g(x1) hasta g(x2), se tiene:
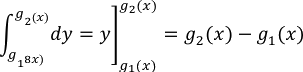
Combinando esas dos integrales, se puede expresar el área de R como la integral iterada:
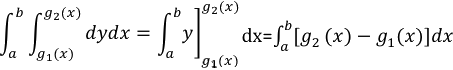
La región acotada por: a≤x≤b y g(x1)≤y≤g(x2)
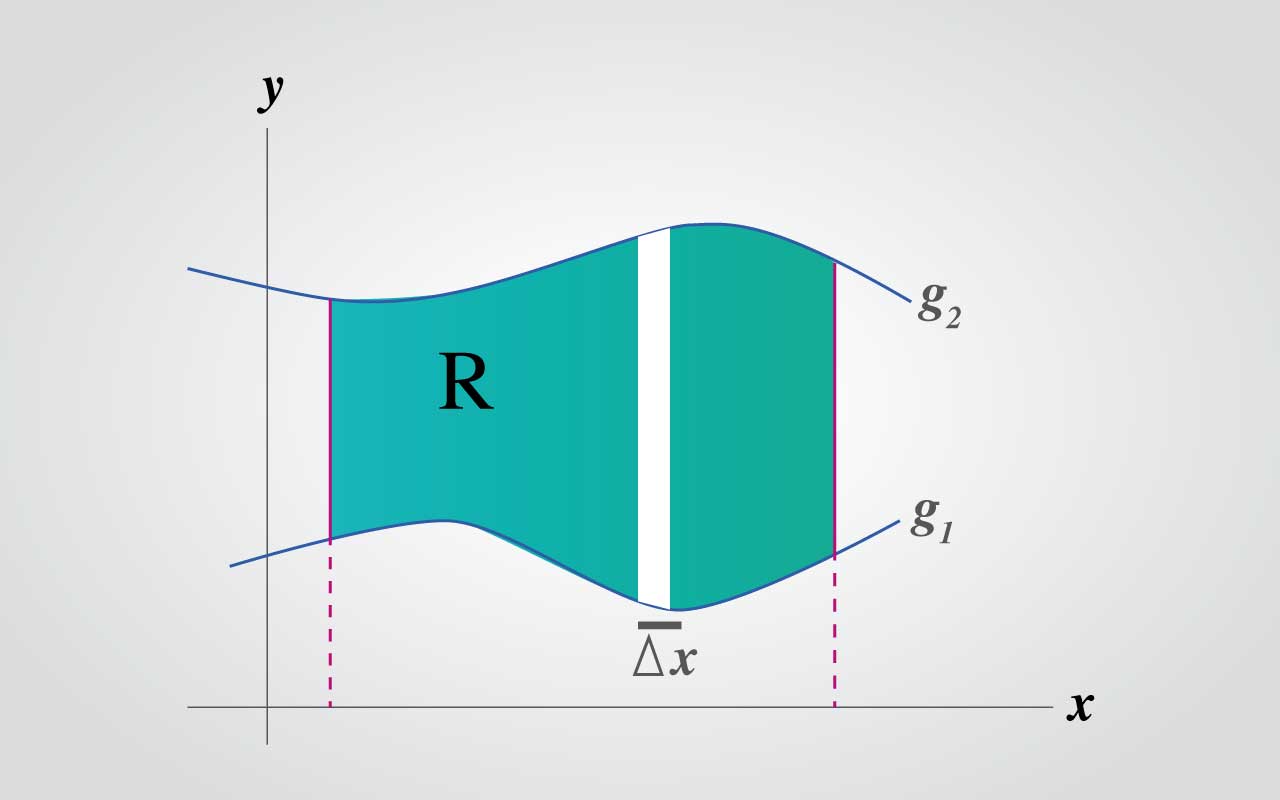
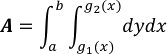
Análogamente, un rectángulo horizontal implica el orden dydx, con los límites interiores determinados por las cotas izquierda y derecha del rectángulo de la figura. Una región de esta clase se llama horizontalmente simple, ya que los límites exteriores son las rectas horizontales =ce y=d. Las integrales iteradas en los dos tipos de regiones se resumen en lo siguiente:
1. Sí R está definida por
donde g1,g2 son continuas en [a,b] m el área de R viene dada por:
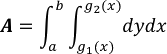
2. Sí R está definida por
donde h1,h2 son continuas en [c, d], el área de R viene dada por:
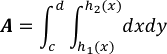
La región está acotada por: c≤y≤d, h1(y)≤x≤h2(y)
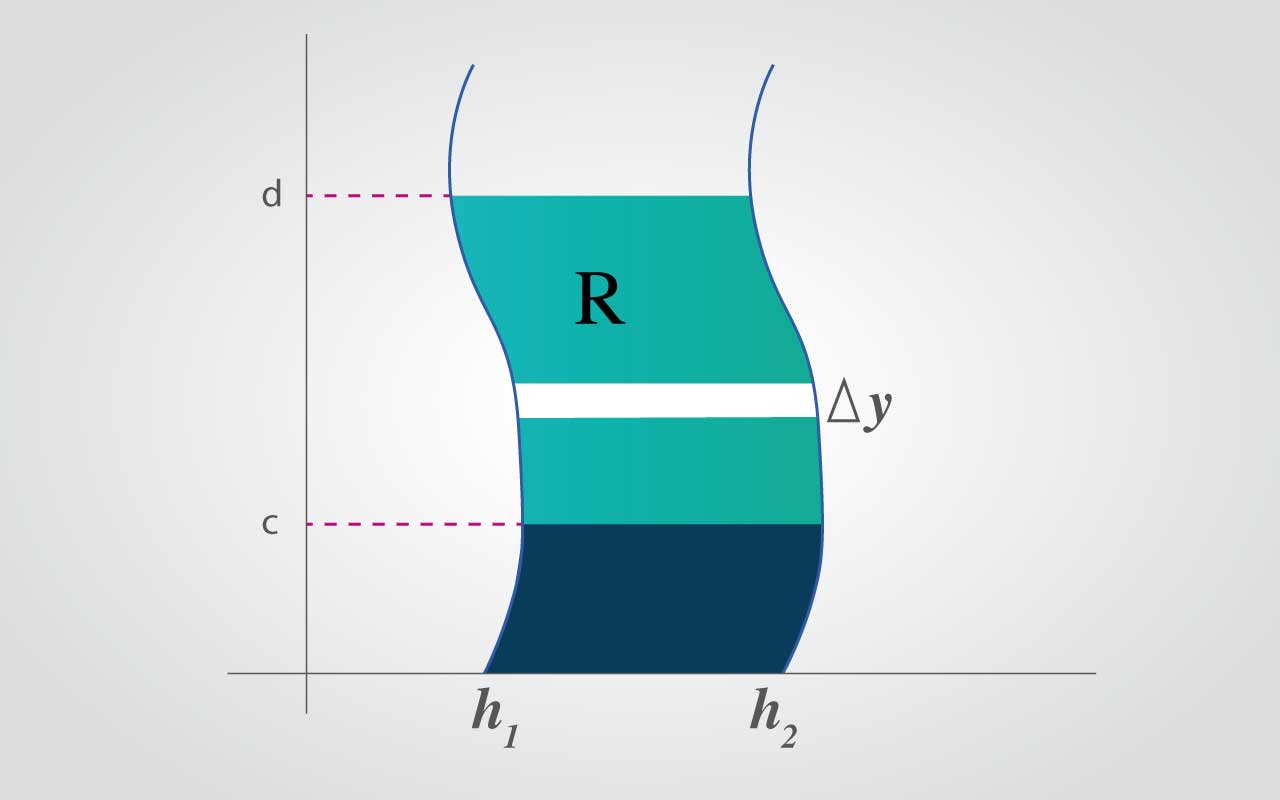
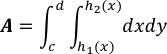
Nota: debe convencerse que aquel orden en esas dos integrales es diferente: dydx para regiones verticalmente simples y dxdy para regiones horizontalmente simples.
Si los cuatro límites son constantes, la región de integración es rectangular, como muestra el ejemplo 2.
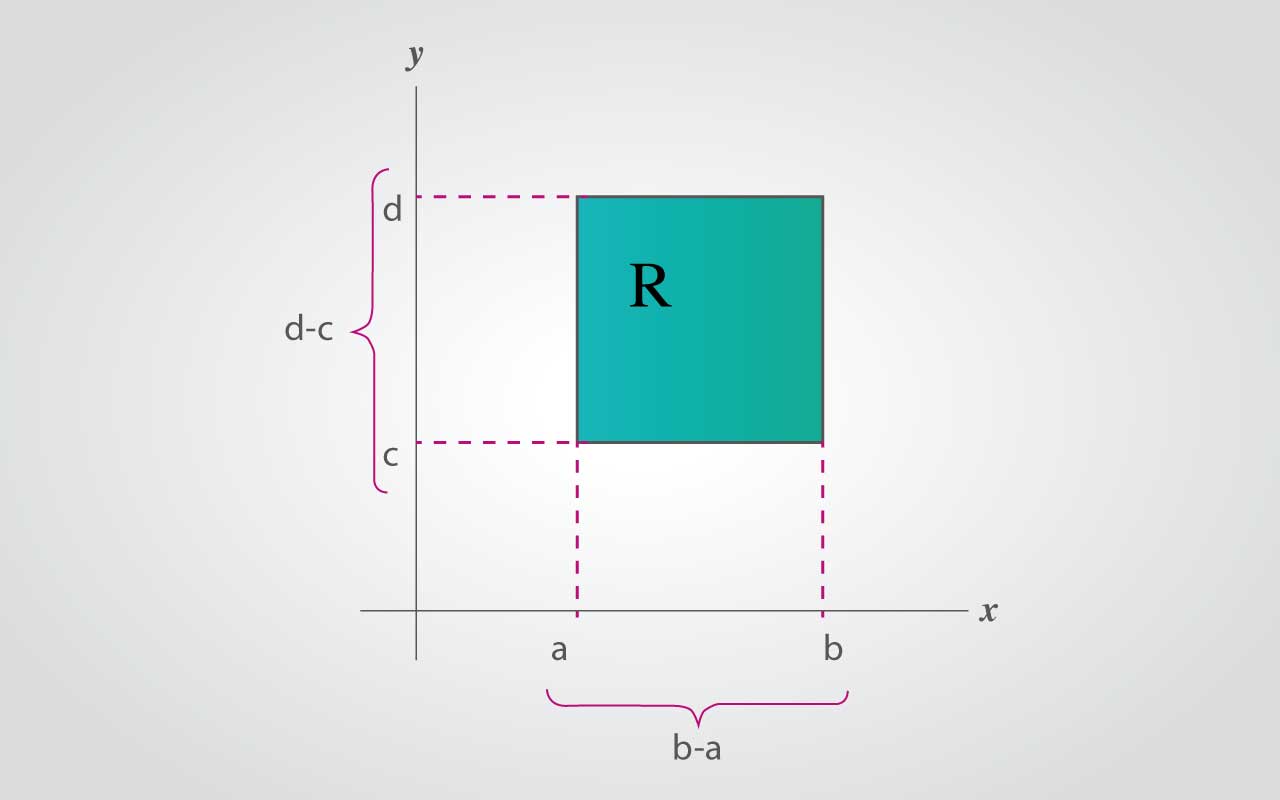
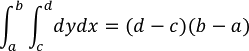
Representar mediante una integral iterada el área del rectángulo de la figura anterior.
Solución:La región de la figura es simple verticalmente y horizontalmente, de manera que se puede utilizar cualquiera de los órdenes de integración. Eligiendo el orden dydx se obtiene:
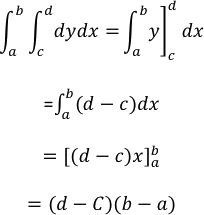
Que era el resultado esperado.
Calcular el área por una integral iterada:
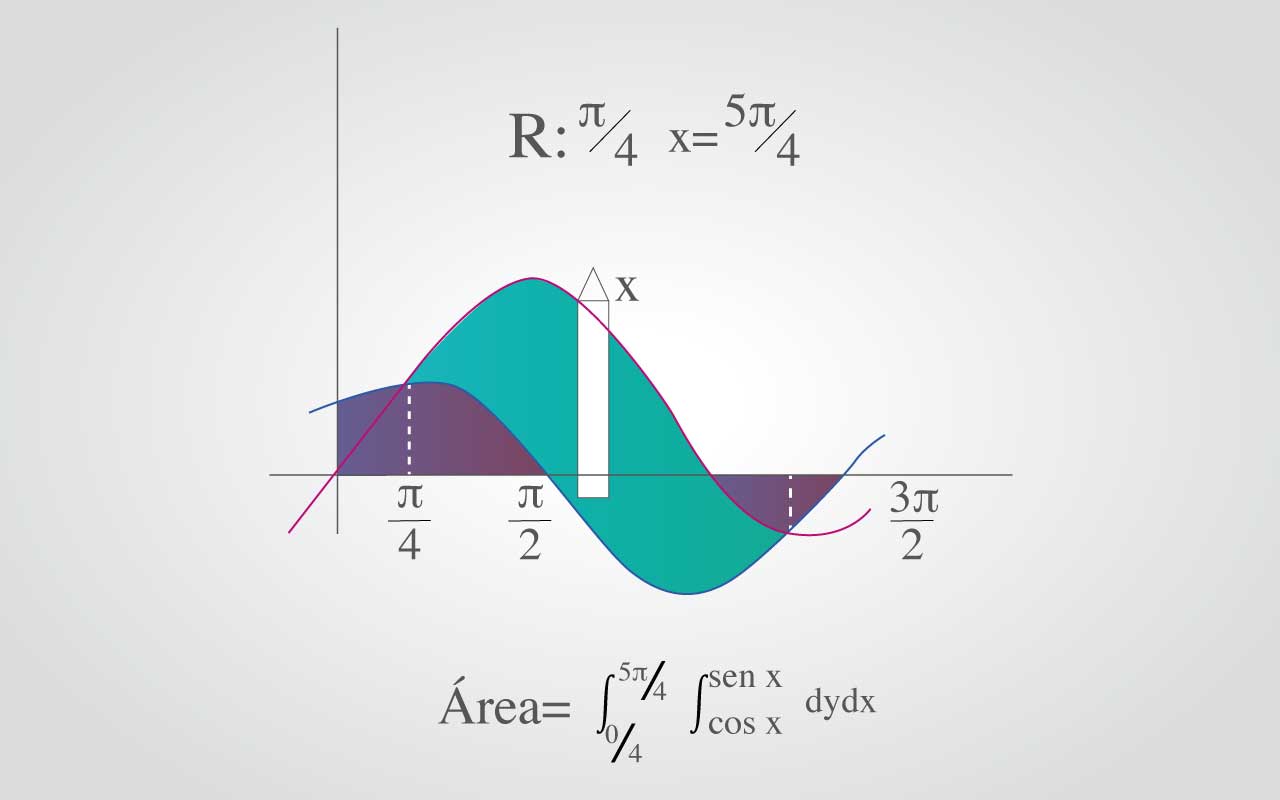
Usar una integral iterada para calcular el área de la región acotada por las gráficas de: f(x)=sen(x) la curva seno es la cota superior; g(x)= cos(x), la curva coseno es la cota inferior.
En el intervalo: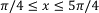
Puesto que f y g vienen dadas como funciones de x , conviene un rectángulo representativo vertical, luego el orden dydx de integración. Los límites exteriores de integración son: 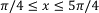 .Además , el rectángulo está acotado superiormente por f(x)=senx e inferiormente por g(x)=cosx, luego:
.Además , el rectángulo está acotado superiormente por f(x)=senx e inferiormente por g(x)=cosx, luego:

La región de integración de una integral iterada no tiene por qué estar acotada por rectas. Por ejemplo la de la figura 24 es verticalmente simple aunque sus fronteras izquierda y derecha no son rectas verticales. Lo que caracteriza a las regiones verticalmente simples es que están acotadas superior e inferiormente por gráficas de funciones de x.
En un problema concreto de integración, uno de los órdenes hará más sencillos los cálculos. Así, sí intenta rehacer el Ejemplo 4 usando el orden dxdy comprobará, con sorpresa, que la tarea es titánica. Ahora bien, si consigue terminarla, la respuesta obtenida será la misma, claro está. En otras palabras, el orden de integración afecta a la dificultad de los cálculos, pero no a su resultado.
Comparación de órdenes de integración distintos.
Dibujar un esbozo de la región cuya área viene dada por la integral:
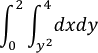
Representar, a continuación, esa misma área mediante una integral con orden deintegración dydx. Verificar que las dos integrales dan el mismo valor para el área.
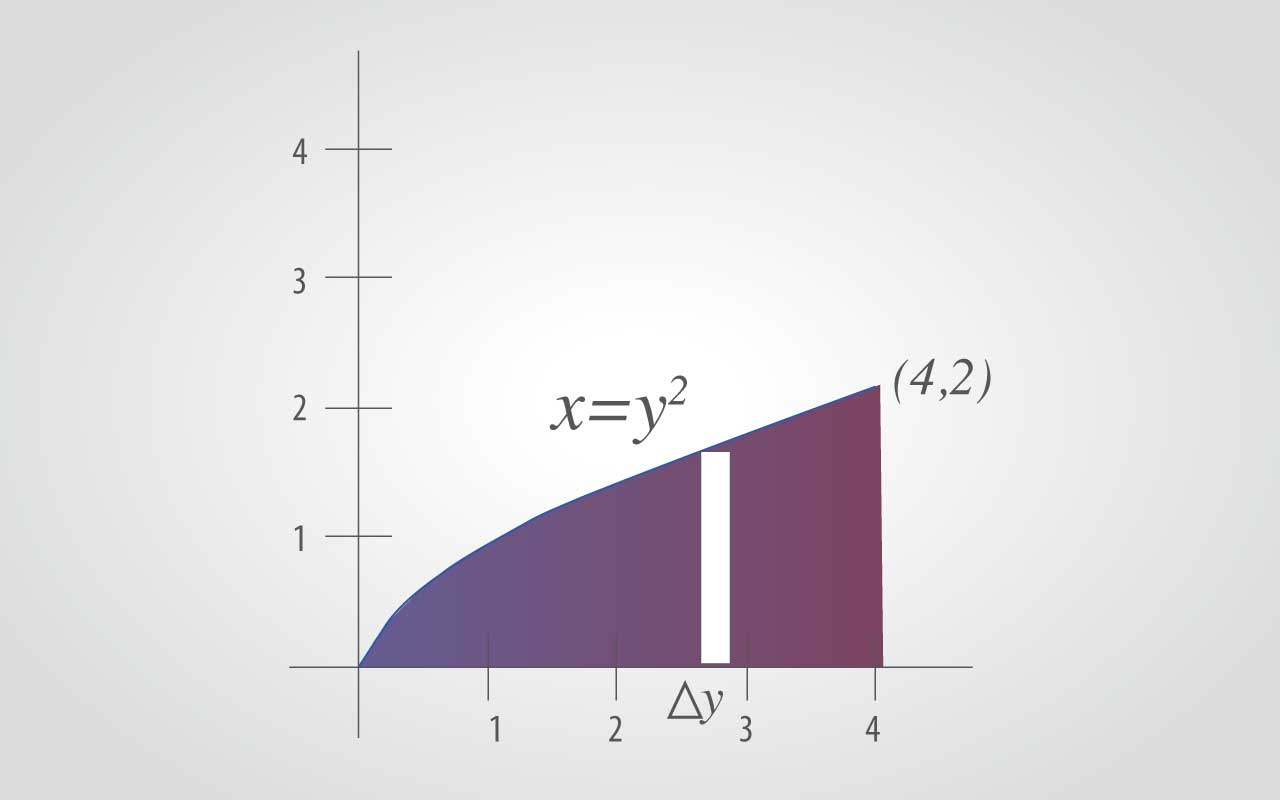
SoluciónA la vista de los límites de integración propuestos: y2≤x≤4 son los interiores de integración. De modo que la región R está acotada a la izquierda por la parábola x=y2 y a la derecha por la recta x=4. Además, como:0≤y≤2 son los límites exteriores de integración.
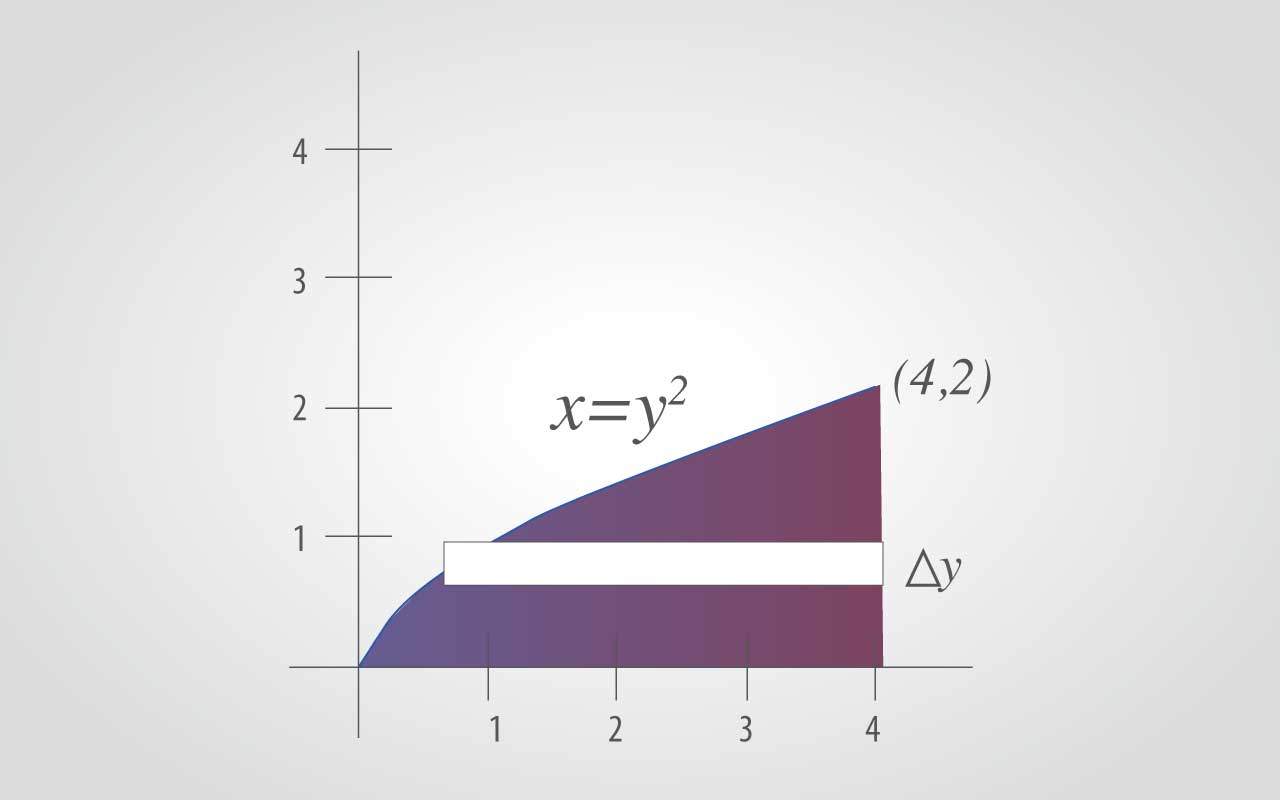
R está acotada por abajo por el eje x. El valor de esa integral es:
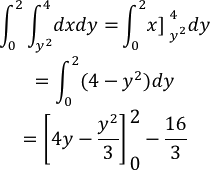
Para cambiar el orden de integración a dydx, se coloca un rectángulo vertical en laregión, de esta forma se ve que las cotas constantes 0≤x≤4 sirven como límites inferiores deintegración. Despejando y en la ecuación x=y2, se concluye que los límites inferiores son: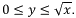 Por tanto, el área de la región se puede presentar por:
Por tanto, el área de la región se puede presentar por:
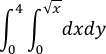
Calculando esta integral, se comprueba que da el mismo valor que la integral original:
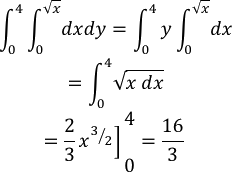
En ocasiones no es posible calcular el área de una región con una única integral. En tales situaciones, se puede dividir la región en subregiones cuyas áreas sean calculables, cada una de ellas, mediante una integral iterada. El área total es simplemente la suma de las integrales iteradas.
Calcular el área dada por la suma de dos integrales iteradas.
La parábola y=4x-x2 es la cota superior, y el eje x, por encima de la recta: y=-3x+6, constituyen la cota inferior.
En la siguiente figura se muestran las funciones acotadas y a calcular su área:

Se comienza partiendo la región R en dos subregiones R1 y R2. En ambas subregiones conviene utilizar rectángulos verticales, de modo que:

El área de la región es 15/2 unidades cuadradas. Intente comprobar el resultado usando el procedimiento de cálculo del área entre dos curvas.
Nota: Es evidente la ventaja que supone disponer de un esbozo de la región de integraciónen los Ejemplo 3 a 6. Se recomienda insistentemente en adquirir el hábito de dibujar la región, ya que es de gran ayuda a la hora de determinar los límites de integración para todas las integrales iteradas de esta unidad.
Calcular:
| 1. | 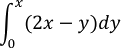 |
| 2. | 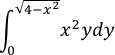 |
| 3. | 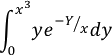 |
| 4. | 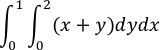 |
| 5. | 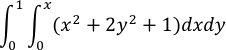 |
| 6. | 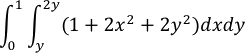 |
[1]Duarte, G. A. (2013). Ejemplos y ejercicios de integrales múltiples. Bogotá.