

Área de una región entre dos curvas. Si f y g son continuas entre [a,b] y g(x)≤f(x), para todo x en [a,b] entonces el área dada región limitada por las gráficas f y g y las líneas verticales x=a y x=b es:
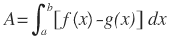
Observe los siguientes ejemplos:
Hallar el área de la región limitada por las gráficas de:
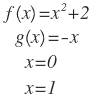
Lo primero que hacemos es graficar f(x) y g(x):

Ahora se hace el cálculo del área de la región sombreada:
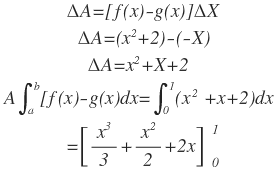
Graficar: f(x) y g(x)
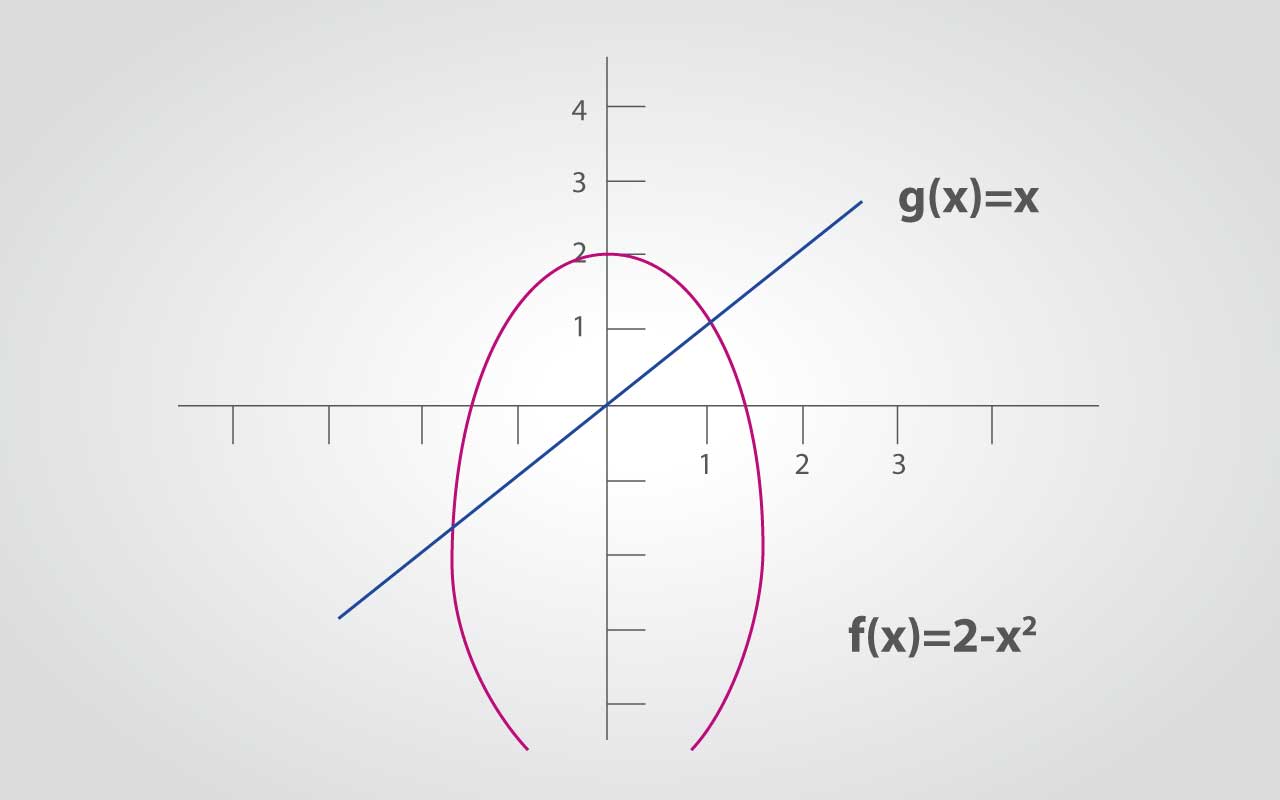
Dado que no se conocen los límites de integración, se procede a buscarlos. Esto se hace igualando las dos funciones:

Estos son los límites de integración:
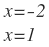
Luego:
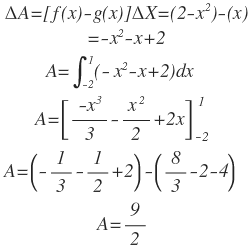
Hallar el área de la región limitada por:
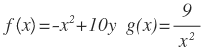
Primero se construye la gráfica:
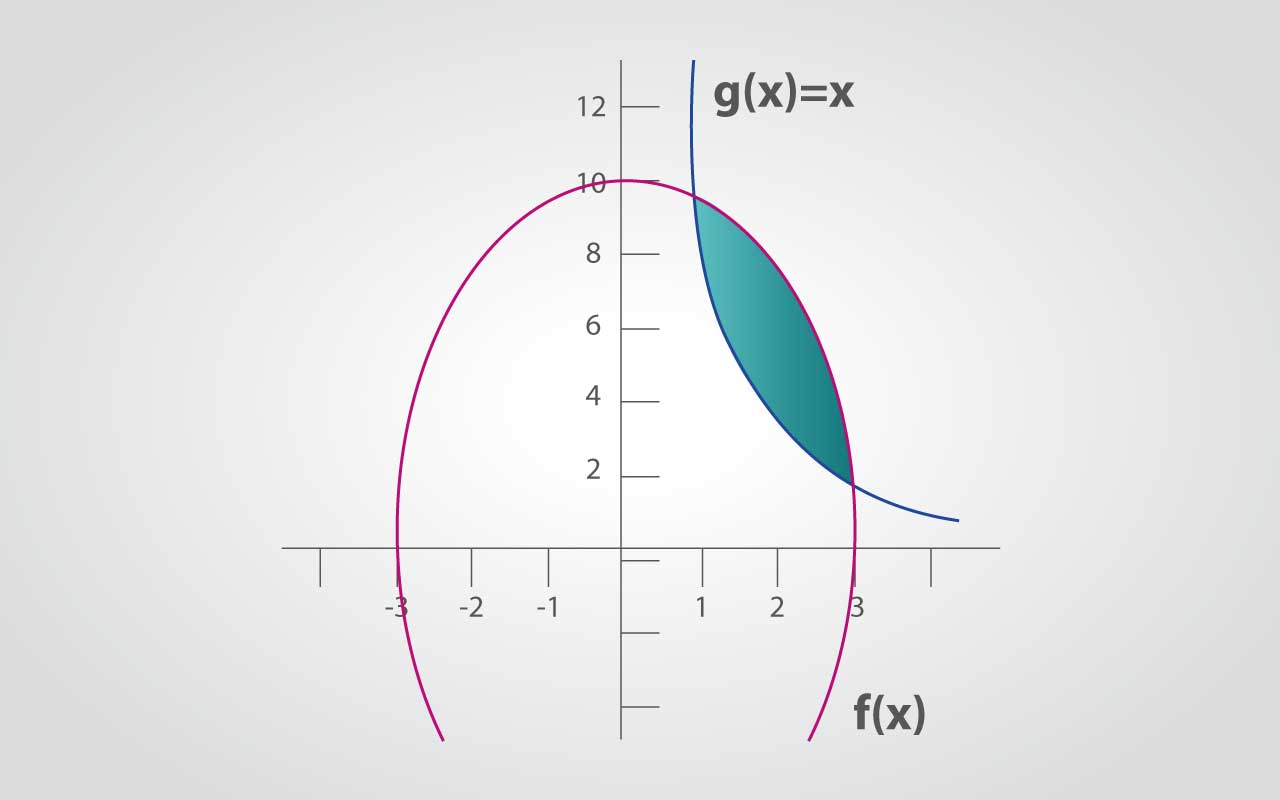
Igualando las funciones:
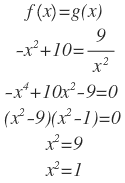
Entonces:
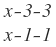
Se toman entonces los valores positivos de x: 3 y 1
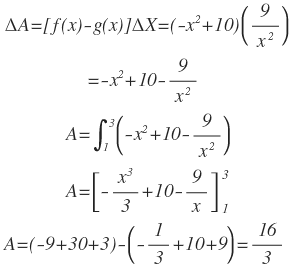
Calcular el área de la región comprendida entre las funciones f(x)= 3x3-x2-10x y g(x)= -x2+2x
Solución:Lo primero que hacemos es graficar f(x) y g(x):

Ahora encontramos los límites de integración igualando las funciones:
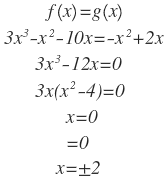
Luego nos toca hacer dos integrales:
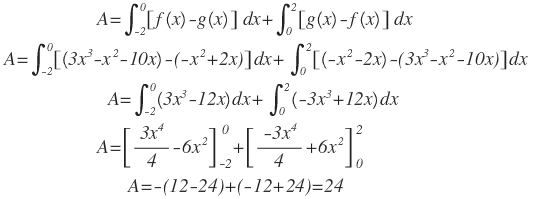
Resuelva los siguientes ejercicios:
Calcular el área de la región dada.
| 1. | 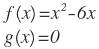 |
| 2. | 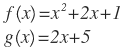 |
| 3. | 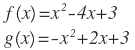 |
| 4. | 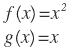 |
| 5. | 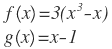 |
| 6. | 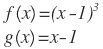 |
[1]Duarte, G. A. (2013). Teorema área de una región. Bogotá.