

En una economía competitiva, gran cantidad de consumidores gastan dinero en algún artículo específico. Por lo general, el precio de ese artículo varía y en muchas ocasiones, el precio es menor que la cantidad total que habría estado dispuesto a gastar. La diferencia entre las dos cantidades puede considerarse como el ahorro logrado por los consumidores y se conoce en economía como excedente o superávit de los consumidores.
De manera similar, en una economía competitiva existen también productores que estarían dispuestos a vender el artículo a un precio menor que el de equilibrio de mercado que los consumidores en realidad pagan. En tal situación, los productores también se benefician; este beneficio se denomina superávit o excedente del productor.
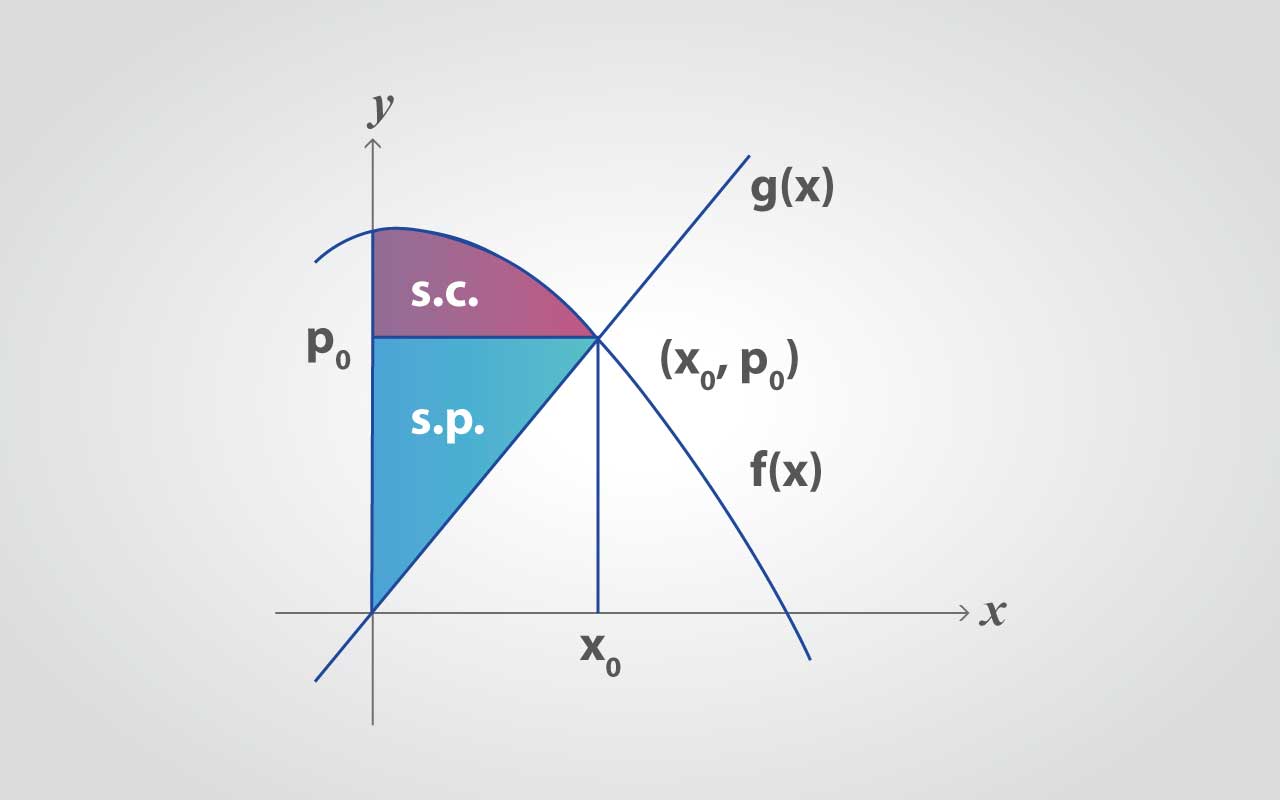
Gráficamente se puede representar el superávit del consumidor y del productor, teniendo en cuenta que p = f(x) es la ecuación de demanda; que p = g(x) es la ecuación de la oferta y el punto de equilibrio en f(x) y g(x) es (Xo, Yo ).
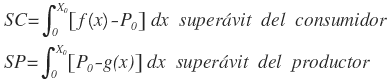
Hallar el excedente o superávit del consumidor y del productor sabiendo que:

Lo primero que hay que hacer es graficar e identificar las ecuaciones de oferta y demanda.
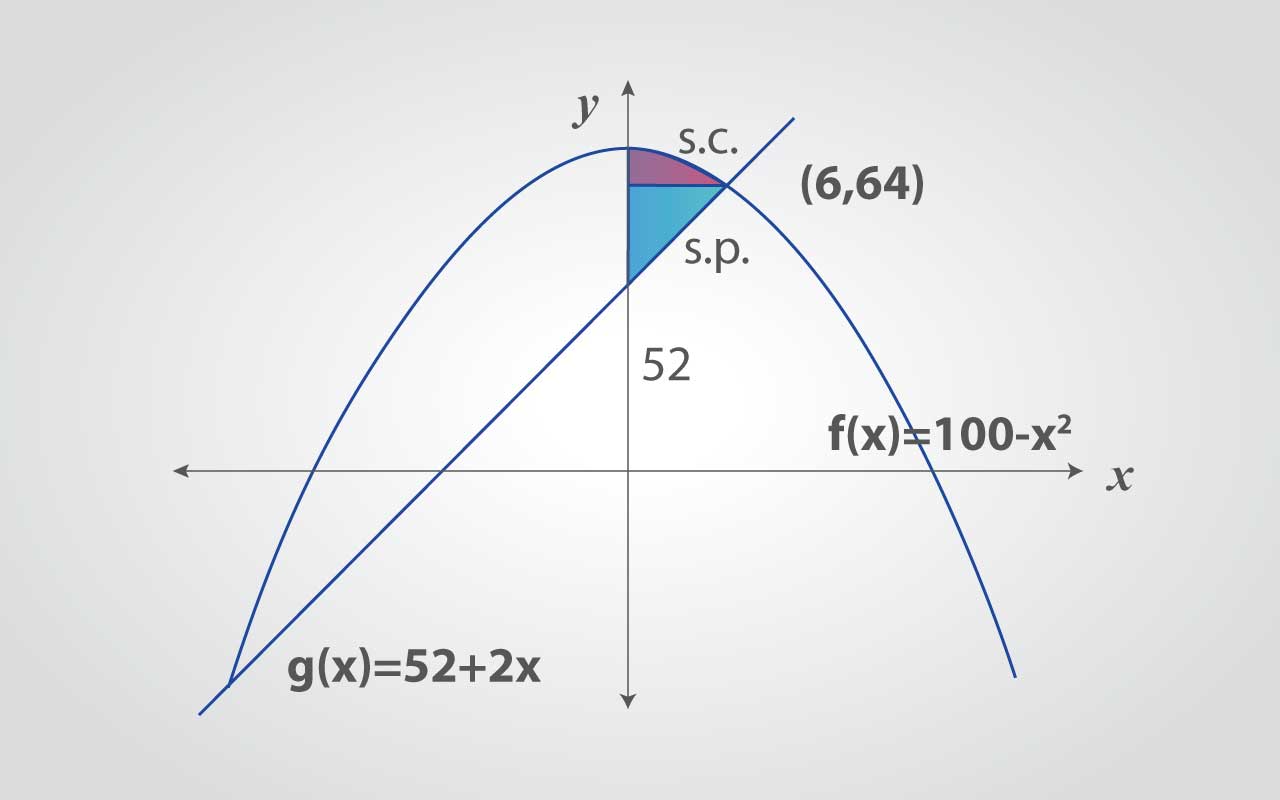
El superávit del consumidor y del productor se trabajará únicamente en el primer cuadrante, ya que las unidades producidas y los precios siempre son positivos.
Se halla el punto de equilibrio entre la oferta y la demanda. Igualando las ecuaciones se tiene que:
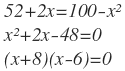
x=-8 x=6 se escoge el valor positivo.
Si x =6 reemplazando en cualquiera de las dos ecuaciones se obtiene:
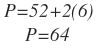
El punto de equilibrio es: (6,64)

El ahorro de los consumidores es de 144 unidades monetarias. Como el superávit del productor se obtiene aplicando:
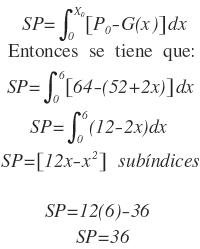
El beneficio de los productores es de 36 unidades monetarias.
Las ganancias netas generadas por cierta maquinaria industrial o la explotación de minas o perforación de pozos durante determinado periodo, es la diferencia entre el ingreso total generado por la maquinaria y el costo total de la operación y el mantenimiento de esta.
Supóngase que cuando tiene t años cierta maquinaria industrial o la explotación de minas o perforación de pozos durante determinado periodo, es la diferencia entre el ingreso total generado por la maquinaria y el costo total de la operación y el mantenimiento de esta.
Supóngase que cuando tiene x años, cierta maquinaria industrial genera ingresos a razón de:
R”(X)= 5.000 -20X2 unidades monetarias por año y costo que se acumulan a razón de:
C”(X)= 2000+102 unidades monetarias por año.
1.¿Durante cuántos años es rentable el uso de la maquinaria?
2.¿Cuáles son las ganancias netas generadas por la maquinaria durante el periodo?
Solución:a.El uso de la maquinaria será rentable en tanto la razón (derivada) genere ingresos, o sea, estos sean superiores a la razón a la que se acumulan los costos.
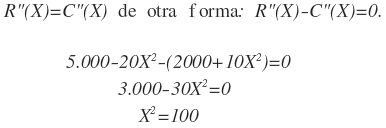
Luego X=±10 se toma el valor positivo, luego se tiene que: x=10 años.
b.Se halla la utilidad máxima en el periodo de 10 años.
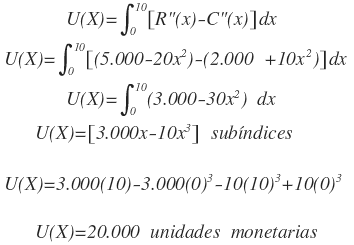
Luego, la utilidad obtenida durante el periodo de 10 años es de 20.000 unidades monetarias.
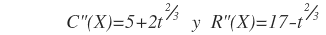
En donde C y R se miden en millones de pesos y t en años. Determine qué tanto deberá prolongarse la operación y encuentre la utilidad total que puede obtenerse durante este periodo.
Solución:
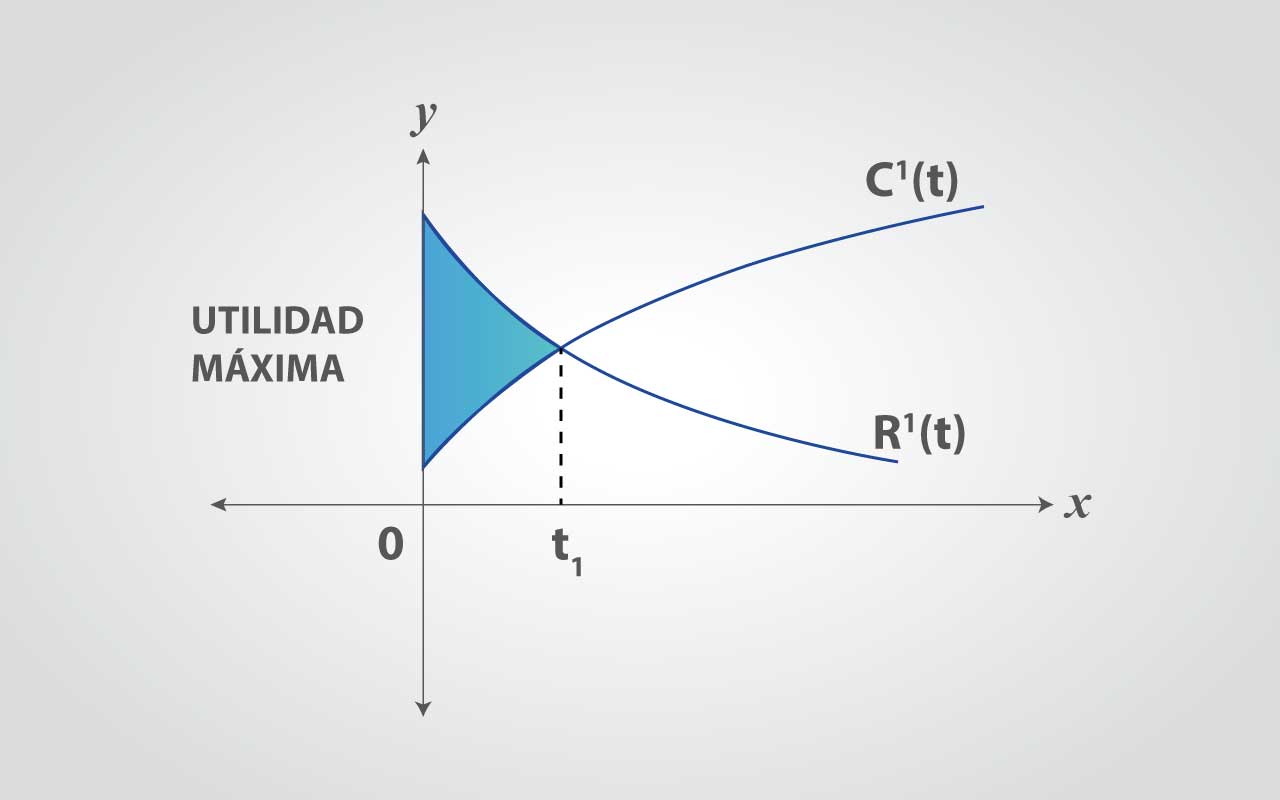
El instante t1 que, dará como resultado la utilidad máxima es el instante en que el costo y el ingreso son iguales. Es decir:

En consecuencia, la operación deberá mantenerse por t1 = 8 años. La utilidad que puede observarse durante este periodo de 8 años está dada por:
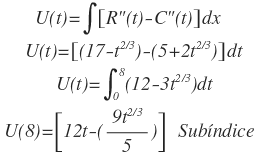
U (8)=38.8 millones de pesos.
Determínese el superávit del consumidor y del productor en el caso de un producto cuyas funciones de demandan y de oferta aparecen enseguida.(suponga que se ha establecido el equilibrio del mercado).
| 1. |  |
| 2. |  |
| 3. | 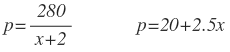 |
| 4. |  |
| 5. | 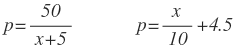 |
6. Supóngase que cuando se tiene x años, una maquinaria industrial genera ingresos a razón de R”(x) = 6.02 5 – 10x2 pesos por año y originan costos que se acumulan a la razón de C”(x) = 4.000 +15x2 pesos por año.
a. ¿Durante cuántos años es rentable el uso de la maquinaria?
b. ¿Cuáles son las ganancias netas generadas por la maquinaria durante el periodo hallado en el literal a?
7. Las tasas de ingreso y el costo en una operación de perforación petrolera están dadas por los siguientes datos:
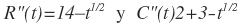
Respectivamente, en donde el tiempo t se mide en años y C se mide en millones de pesos.¿Cuánto deberá prolongarse la perforación a fin de obtener la utilidad máxima? ¿Cuál es esta utilidad máxima?
Respuesta:
1. SC = 16 SP = 8ss
2. SC = 8.000 SP = 16.000/3
3. SC = 178.16 SP = 45
4. SC = 25.6 SP = 38.4
5. SC = 50Ln 2 SP = 1.25
6. a) 12 años b) $1.008
7. a) 9 años b) $36 millonesReferencia[1]
[1] Duarte, G. A. (2013). Aplicaciones de la integral definida. Bogotá.