

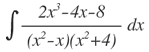
Como:

Se incluye una fracción por cada factor:
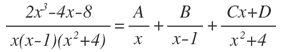
Ahora nos toca hallar los valores de A, B, C y D:
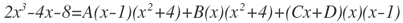
Si queremos hallar el valor de A, entonces x=0
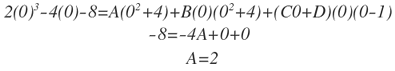
Para hallar el valor de B, entonces x=1
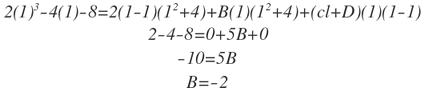
Para hallar el valor de C y D, construimos 2 ecuaciones lineales, cuando x=2 y x=-1. Como ya conocemos el valor de A y B.
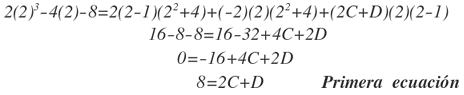
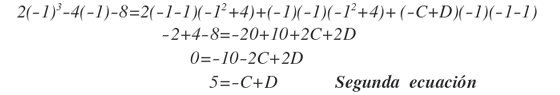
Tomamos la primera y segunda ecuación y las resolvemos:
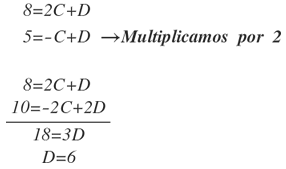
Si:
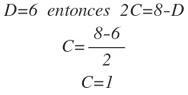
Ahora si podemos integrar:
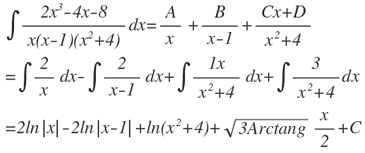
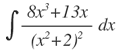
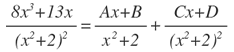
es decir que:

Agrupando por grado:
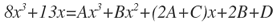
Igualando por grados:
8x3=Ax3, es decir que A=8
0x2=Bx2, es decir que B=0
13x=(2A+C)x,como A=8,entonces se tiene:13=2*8+C,es decir que:C=-3
0=2B+D,pero B=0,osea que D=0.
En estas condiciones, sustituyendo las letras:
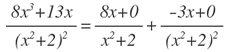
luego la integral es de la forma:
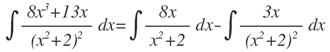
Aplicando los métodos conocidos:
Para: ∫8x/x2+2 dx, haciendo u=x2+2, du=2xdx, es decir que 4du=8xdx.
Es decir que:
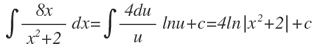
Para:∫3x/(x2+2)2 dx, haciendo u=x2+2,du=2xdx,por lo tanto:3du/2=3xdx.
Sustituyendo en la integral se tiene:

Ahora reuniendo toda la expresión, se obtiene:
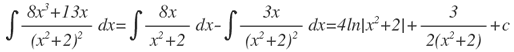
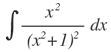
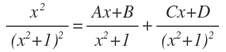
Luego:
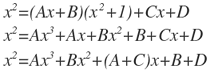
Igualamos por grados:
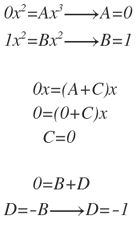
Entonces:
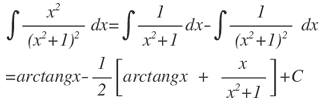
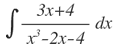
Como:
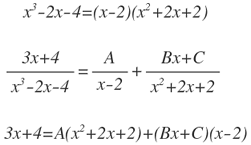
Para calcular el valor de A, x=2
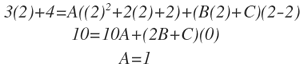
Para calcular el valor de C, x=0
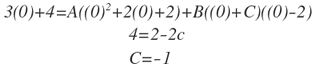
Para calcular el valor de B, x=1
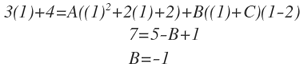
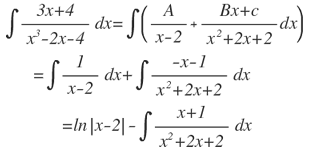
para integrar esta última expresión: u=x2+2x+2,du=2(x+1)dx
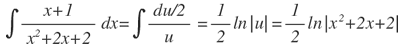
Luego:
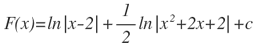
| 1. | 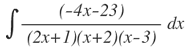 |
| 2. | 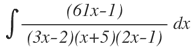 |
| 3. | 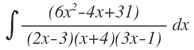 |
| 4. |  |
| 5. | 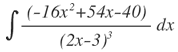 |
| 6. | 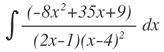 |
| 7. | 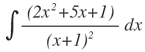 |
| 8. | 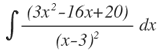 |
| 9. | 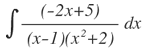 |
| 10. | 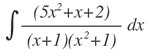 |
| 11. | 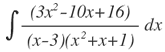 |
[1] Duarte, G. A. (2013). Factores cuadráticos. Bogotá.