Ejemplos y ejercicios de integración por partes

Ejemplo 1

Haciendo u=x, dv=senx dx, se calcula du=dx, v=∫senx dx=-cosx

Aplicando la ecuación:

Ejemplo 2

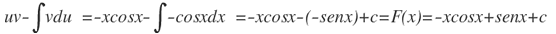
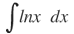
Haciendo u=ln(x), dv=dx, se halla: du=dx/x , v=∫dx=x

Aplicando la ecuación:

Ejemplo 3

Haciendo u=x2, dv=senx dx, se calcula du=2xdx, v=∫senx dx=-cosx

Aplicando la ecuación:

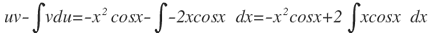
Nuevamente hay que aplicar la fórmula de integración por partes sobre la expresión:

Haciendo u=x, dv=cosx dx, se calcula du=dx, v=2∫cosx dx=-2senx

Aplicando la ecuación:

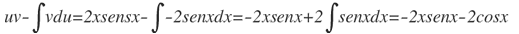
Ahora reuniendo toda la expresión, se obtiene:

Ejemplo 4

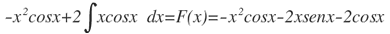
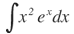
Haciendo u=x2, du=2xdx, y, dv=exdx; de donde: v=ex

Aplicando la ecuación:

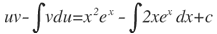
Nuevamente hay que aplicar la fórmula de integración por partes sobre la expresión:

Haciendo: u=2x, du=2dx; dv=exdx; de donde: v=ex

Aplicando la ecuación: u

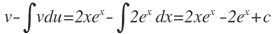
Ahora reuniendo toda la expresión, se obtiene:

Ejemplo 5

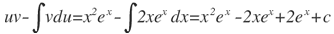
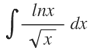
Haciendo u=lnx, du=dx/x; dv=dx/x1/2, ∫dv=∫x-1/2dx, así que v=2x1/2

Aplicando la ecuación:

Ejemplo 6

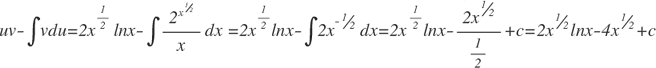
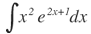
Haciendo u=x2, du=2xdx, y, dv=e2x+1dx; de donde: v=e2x+1/2

Aplicando la ecuación:

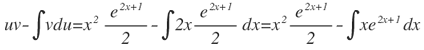
Nuevamente hay que aplicar la fórmula de integración por partes sobre la expresión:

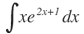
Haciendo: u=x, du=dx; dv=e2x+1dx, v=e2x+1/2

Aplicando la ecuación:

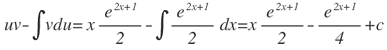
Ahora reuniendo toda la expresión, se obtiene:

Ejercicios

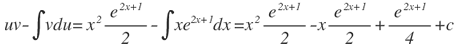
Resuelva los siguiente ejercicios aplicando la técnica de integración por partes.

1.
2.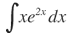
3.
4.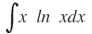
5.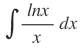
6.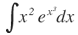
7.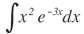
8.
9.
10.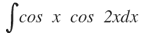
11.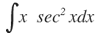
12.
12.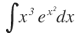
12.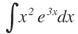

[1] Duarte, G. A. (2013). Ejemplos y ejercicios de integración por partes. Bogotá.