Integración por sustitución

Este método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.

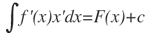
Para cambiar de variable se identifica una parte de lo que se va a integrar con una nueva variable u, de modo que se obtenga una integral más sencilla.

Ejemplo 1

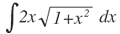
Haciendo el cambio: u= 1+x², y derivando u, se tiene: du=2xdx, es decir que: dx=du/2x.

Sustituyendo:

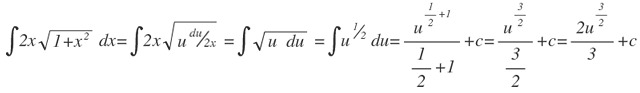
Sustituyendo nuevamente en términos de x, pues u=1+x², se obtiene que:

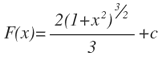
Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejemplo 2

Haciendo el cambio: u=2x+1, y hallando du= 2dx, es decir que: dx=du/2.

Sustituyendo por u:

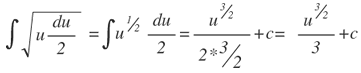
Sustituyendo por x, dado que u=2x+1, se obtiene:

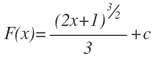
Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejemplo 3

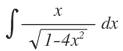
Haciendo el cambio: u= 1-4x², y hallando du= -8xdx, es decir que dx= -du/8x.

Sustituyendo en la integral se tiene:

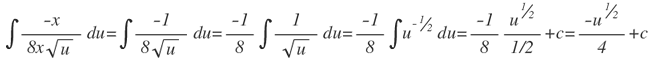
Sustituyendo por x dado que u= 1-4x², se obtiene:

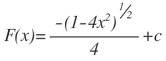
Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejemplo 4

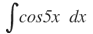
Haciendo el cambio: u=5x, y hallando du=5dx, de donde: dx=du/5.

Sustituyendo en la integral, se tiene:

Sustituyendo en x, dado que u=5x, se obtiene:

Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejemplo 5

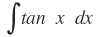
Aplicando la identidad trigonométrica:

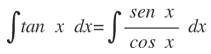
Sustituyendo u= cos x, y derivando: du=-sen x dx, se obtiene: dx= -du/sen x.

Sustituyendo en la integral:

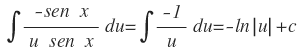
Sustituyendo por x se obtiene:

Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejemplo 6

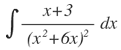
Haciendo el cambio: u= 6x+x², derivando: du= (6+2x)dx, factorizando: du=2(3+x)dx, es decir que: (3+x)dx=du/2.

Sustituyendo en la integral se obtiene:

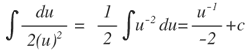
Sustituyendo en x:

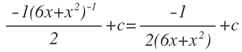
Ejercicio: derive el resultado de F(x), para encontrar f(x).

Ejercicios

Resuelva los siguientes ejercicos aplicando la técnica de integración por sustitución:

1.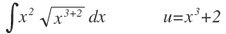
2.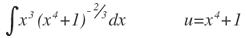
3.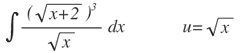
4.
5.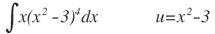
6.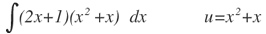
7.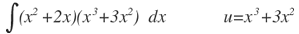
8.
9.
10.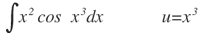
11.
12.

[1] Duarte, G. A. (2013). Fórmulas de integración. Bogotá.