Si se tiene una función F(x) la cual se deriva obteniéndose f(x) en un intervalo i cualquiera se dece que F(x) es la anti-derivada de f(x), esto se expresa como: F’(x)=f(x) donde F(x) es la anti-derivada de f(x). Para comprender mejor este concepto, vease el siguiente ejemplo:
Si se sabe que d/dx(senx) = cosx, entonces se tienes que senx es la anti-derivada de cosx y por tanto F(x)= senx y f(x)=cosx, entonces lo que se pretende ahora es que partiendo de f(x) se puedadeterminar a F(x).
Si piden encontrar la anti-derivada de f(x)=2x, puede existir varias funciones que son anti-derivadas como por ejemplo F(x)=x2+1 ya que si se deriva esta función se obtiene f(x)=2x ó f(x)=x2-4 ya que si se deriva a esta función también se obtiene f(x)=2x, como se acaba de observar puede existir infinitas anti-derivadas para alguna función en particular, en este caso se puede decir, de manera general que la anti-derivada de f(x)=2x es F(x)=x2+c, donde c es una constante.
Existen mecanismos para encontrar la anti-derivada de una función, se citaran algunos de los más comunes. En adelante cuando se quiera representar la anti-derivada de una función lo que se debe hacer es poner una ∫f(x)dx antes de la función, este símbolo se le conoce como integral indefinida, el dx se conoce como diferencial y se utiliza para saber con respecto a que variables se está hallando la anti-derivada. Teniendo en cuenta lo dicho notese que la anti-derivada de una función elevada a la n, es decir ∫(xn)dx= xn+1/n+1 + c, se puede comprobar que esta es efectivamente la fórmula ya que si se deriva el término de la derecha se obtiene la función xn, tal cual se mostró en la introducción.
Si F(x) es una anti-derivada de f(x) sobre un intervalo I, entonces la anti-derivada más general de f(x) es: F(x)+c, donde c es una constante.
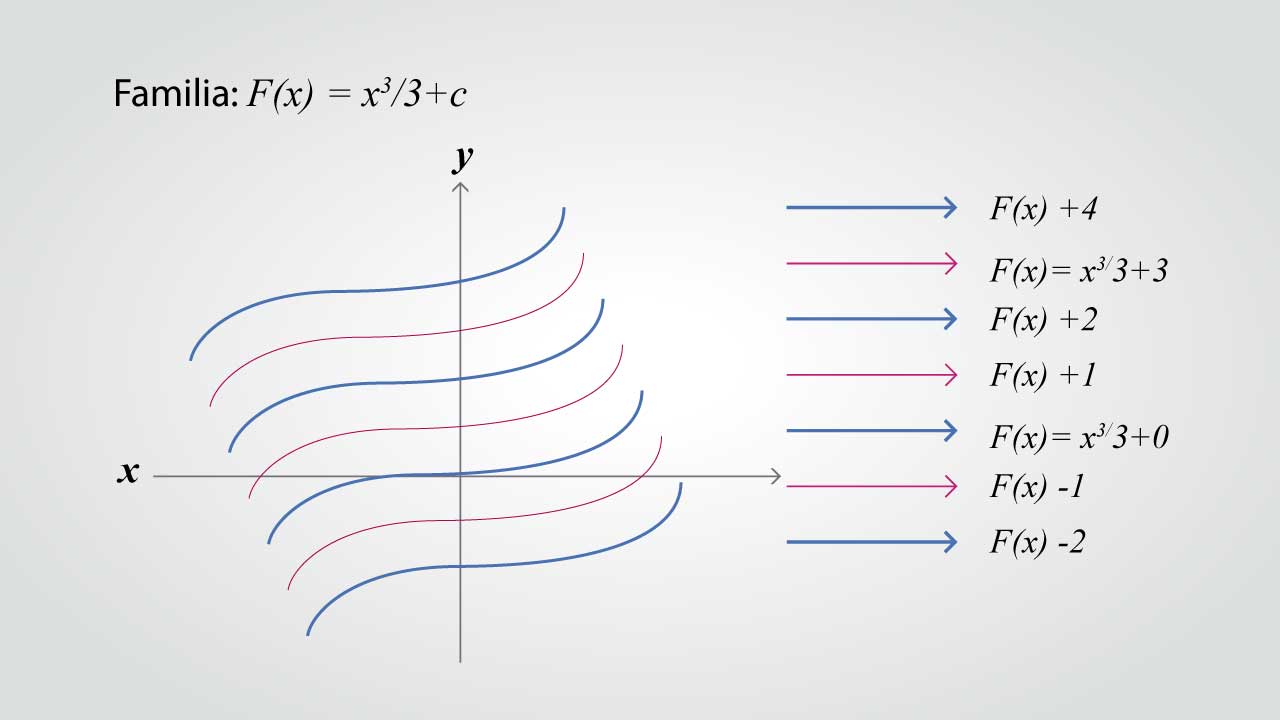
Si f(x)=x2, la anti-derivada general corresponde exactamente a la introducción hecha osea: F(x)=x3/3+c. Al asignar valores reales a c, se obtiene una familia de funciones cuyas gráficas son translaciones verticales.