Aplicaciones de la integral

En esta sección se solucionan algunos ejemplos de aplicación sobre ingreso marginal y total.

Una forma de obtener la función de ingreso total es a partir de la integral de la función de ingreso marginal.

Ejemplo 1: Precio

Suponga que el precio de un producto es constante a un valor de $10 por unidad, es decir la función de ingreso marginal es: f(x)= MR= 10. ¿Cuál es el ingreso por la venta de 1500 unidades?

Desde el punto de vista aritmético es una simple multiplicación, es decir 10*1500=$15.000.

Desde el punto de vista geométrico, es el área de un rectángulo, de base la variable independiente (que en este caso es la cantidad de unidades que se venden=1500) y de altura la variable dependiente (que es el precio de venta=$10).

Figura 1. Gráfica de las funciones integrales según el ejemplo 1.

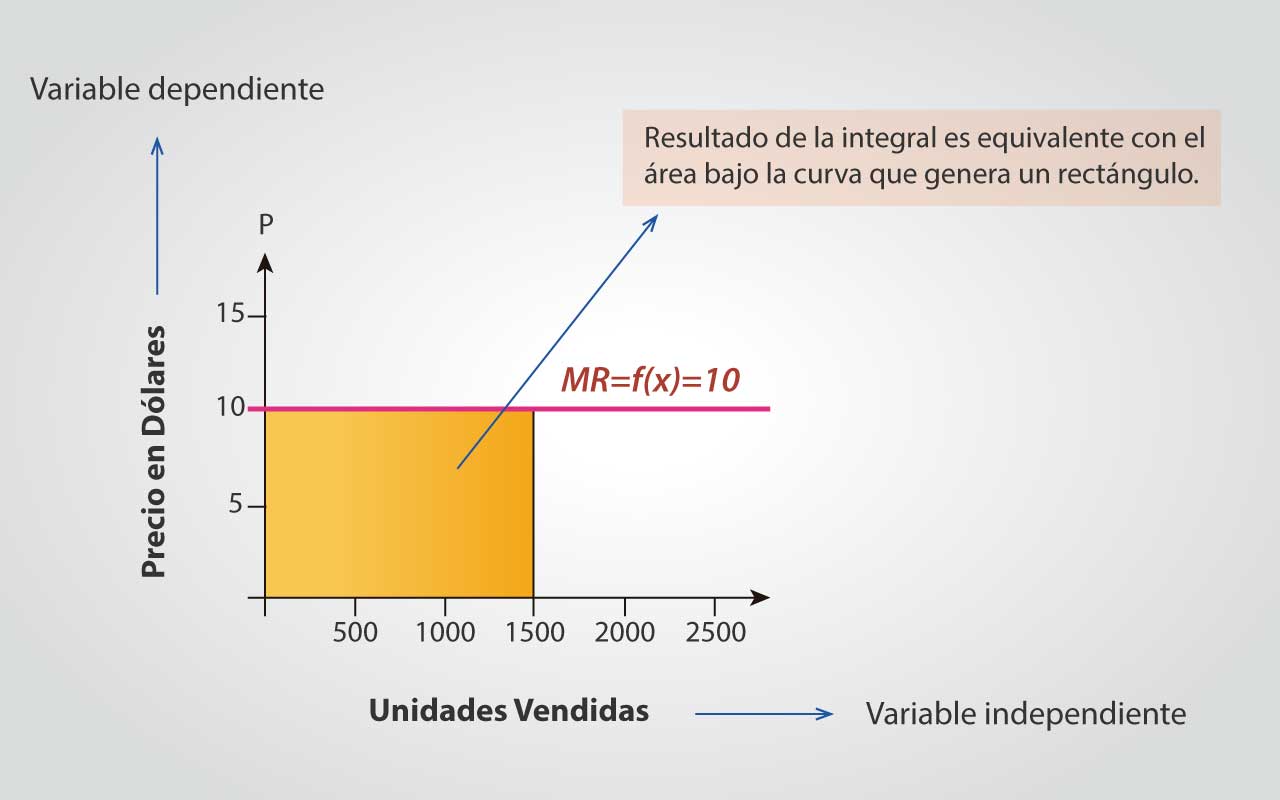
Desde el punto de vista de integrales, es el área bajo la curva, en este caso la curva es una línea recta en el precio de $10, tal cual se ve en la figura 1. Y al calcular la integral se obtiene el área la cual corresponde al ingreso total.

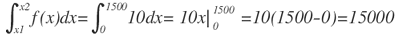
Observe que el resultado es el mismo y no sorprende, pues es el concepto de integral o el teorema fundamental del cálculo el que se está aplicando. Es decir que el ingreso total es de $1500.

Es decir de un ingreso marginal por unidad de $10, se puede hallar el ingreso total por venta de 1500 unidades, que equivale a $15.000. En este caso se trata de un marginal lineal, lo que evidencia que sería más sencillo con la interpretación aritmética, pero cuando este no es lineal, es necesaria la aplicación de integrales.

Ejemplo 2: Gastos

Un administrador de empresas estima que la tasa anual de gastos r(t) de la compañía está representada por la función: r(t)=100+10t2.

Donde t es el año de gasto y r(t) mide la tasa en miles de dólares por año. Con la función de gastos, puede observar que durante el primer año, la tasa de gastos se estiman en: r(1)=100+10(1)2= $110miles USD por año. Para el 3er año la tasa se estima en: r(3)=100+10(3)2= $190 miles de USD.

En la figura 2 se muestra el comportamiento de la tasa de cambio en el tiempo.

Figura 2. Comportamiento de la tasa de cambio en el tiempo.

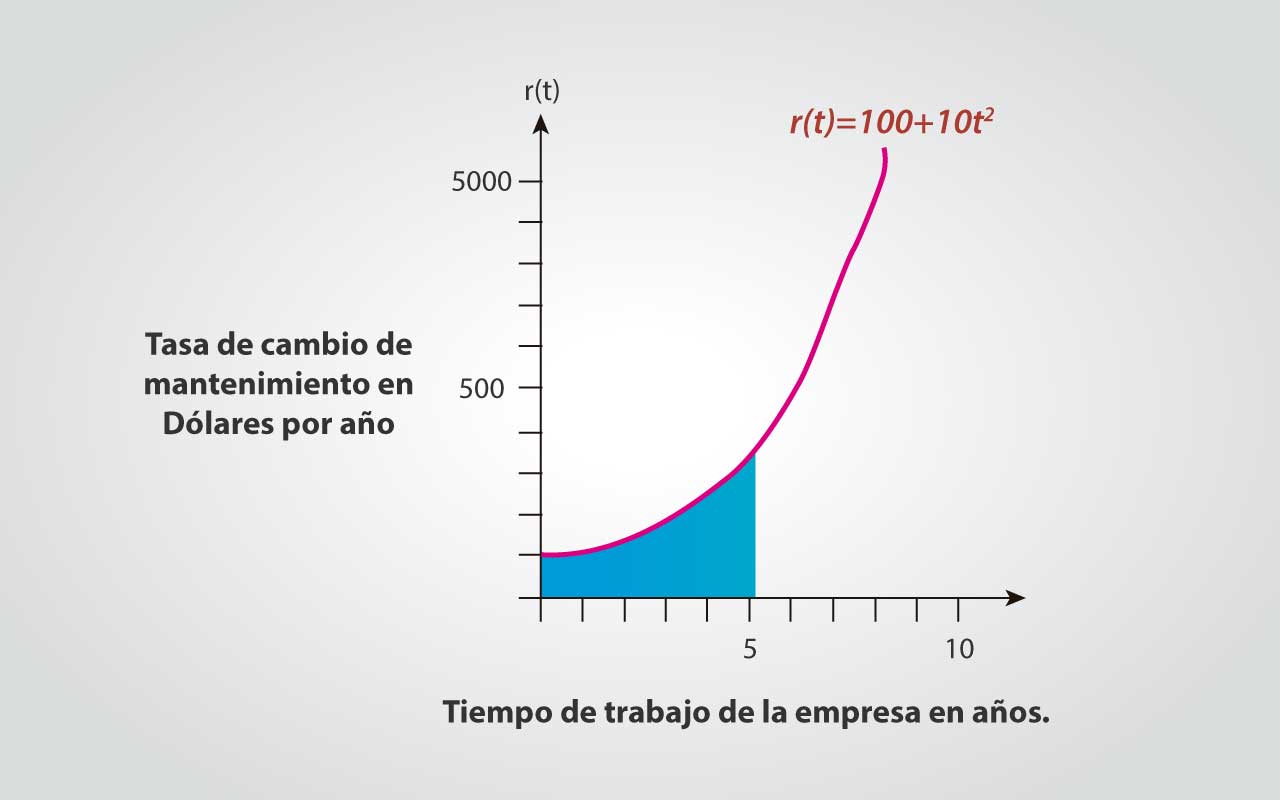
El área bajo la curva representa el costo esperado de los gastos deseados de mantenimiento de la empresa en el tiempo y se calculan con integrales, a saber:

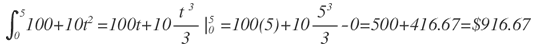
Es decir, se espera que en 5 años el costo de mantenimiento sea de $916.67 miles de usd. Sin embargo podría preguntarse el gasto esperado durante el último año, el cual estaría dado por:

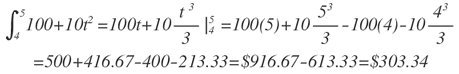
Es decir se espera un gasto de$303.34 miles de USD para el último año.

Ejemplo 3: Recaudación de fondos

Una organización cívica está efectuando su campaña anual de fondos para minusválidos. Los gastos de la campaña se realizarán a una tasa de e(t)=$10.000 usd diarios. Por experiencia se sabe que los aportes serán altos durante las primeras fases de la campaña y con el paso del tiempo disminuirán. La función (figura 3) que describe las donaciones es:

C(t)=-10t2+20.000, donde t representa el día de campaña y c(t) las aportaciones por día.

Figura 3. Gráfica de tasa de gastos y tasa de aportaciones.

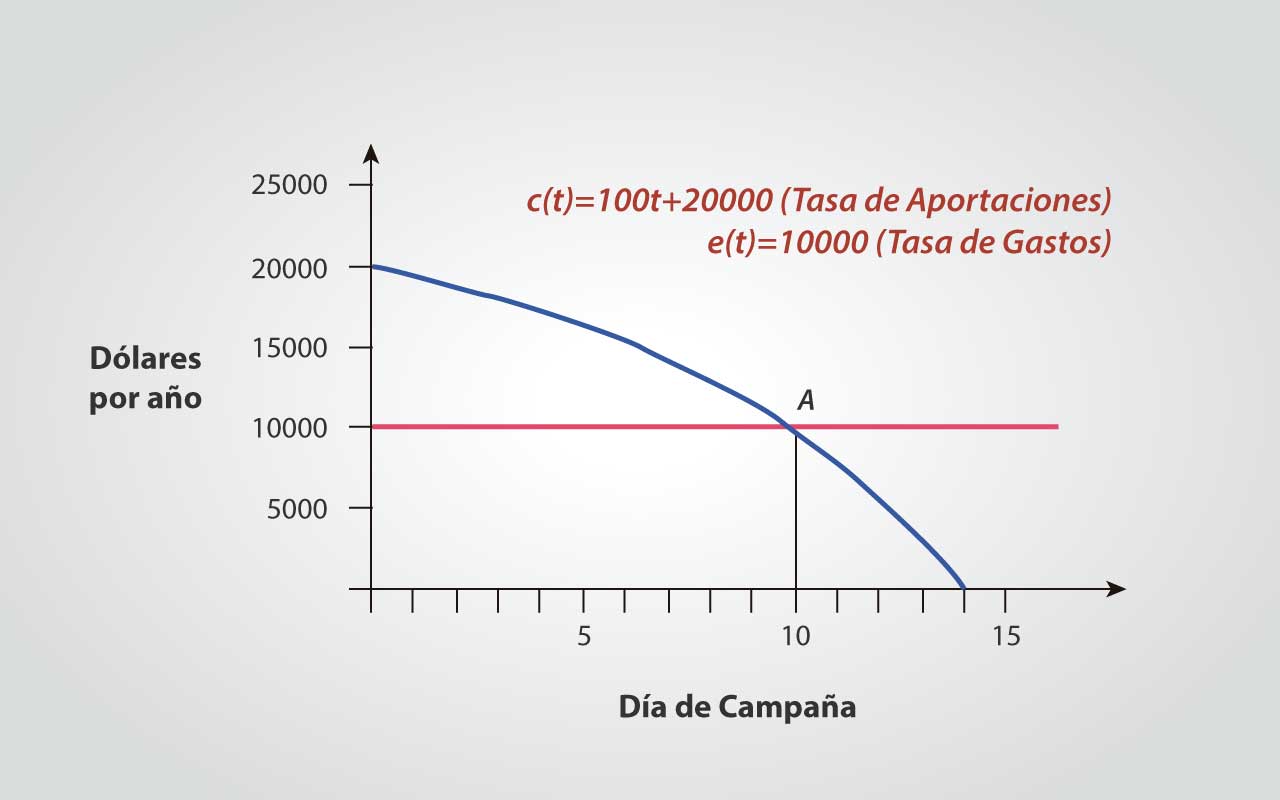
La organización desea maximizar las utilidades netas de la campaña.

1. Determine cuánto debería durar la campaña a fin de maximizar las utilidades netas.
2. ¿Cuáles se espera que sean los gastos totales de la campaña?
3. ¿Cuáles se espera que sean las aportaciones totales?
4. ¿Cuáles se espera que sean las utilidades netas (aportaciones totales menos los gastos totales)?

• La función que describe la tasa a que se realizan los gastos e(t) es:
  

  

  La figura 4 muestra las dos funciones. Mientras la tasa a que hacen los donativos sea mayor que la de los gastos de la campaña, las utilidades netas serán positivas. Éstas serán postitivas hasta que las gráficas de las dos funciones se intersequen. Más allá de este punto, la tasa de gastos excede la tasa de las aporaciones, es decir, los donativos se recibirán a una tasa de menos de $10000 por día. Las dos funciones se intersecan cuando:

  

  O cuando:

  

• Los gastos totales de la campaña están representados por el área bajo e entre t=0 y t=10. Eso podría obtenerse al integrar e entre estos límites o, más simplemente, multiplicando:

  

• Las aportaciones totales durante 10 días están representadas por el área bajo c entre t=0 u t=10, o sea:

  

Ejemplo 4: Administración de bancos de sangre

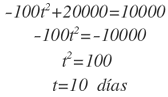
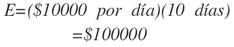
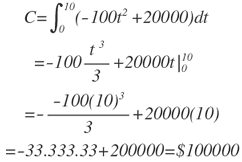
El banco de sangre de un hospital realiza una campaña anual de donación de sangre para reponer su inventario. El hospital estima que se donará sangre a una tasa de d(t) pintas por día donde: d(t) = 500 e-0.4t y t indica la duración de la campaña en días. Si la meta de la campaña es recoger 1000 pintas ¿Cuándo habrá alcanzado esa meta el hospital?

En la figura 4, que representa la función de tasa de donación por día, ya se conoce el área bajo la curva, correspondiente a las 1000 pintas, el problema es el valor t*, necesario para alcanzar esa cantidad.

Figura 4. Representación la función de tasa de donación por día.

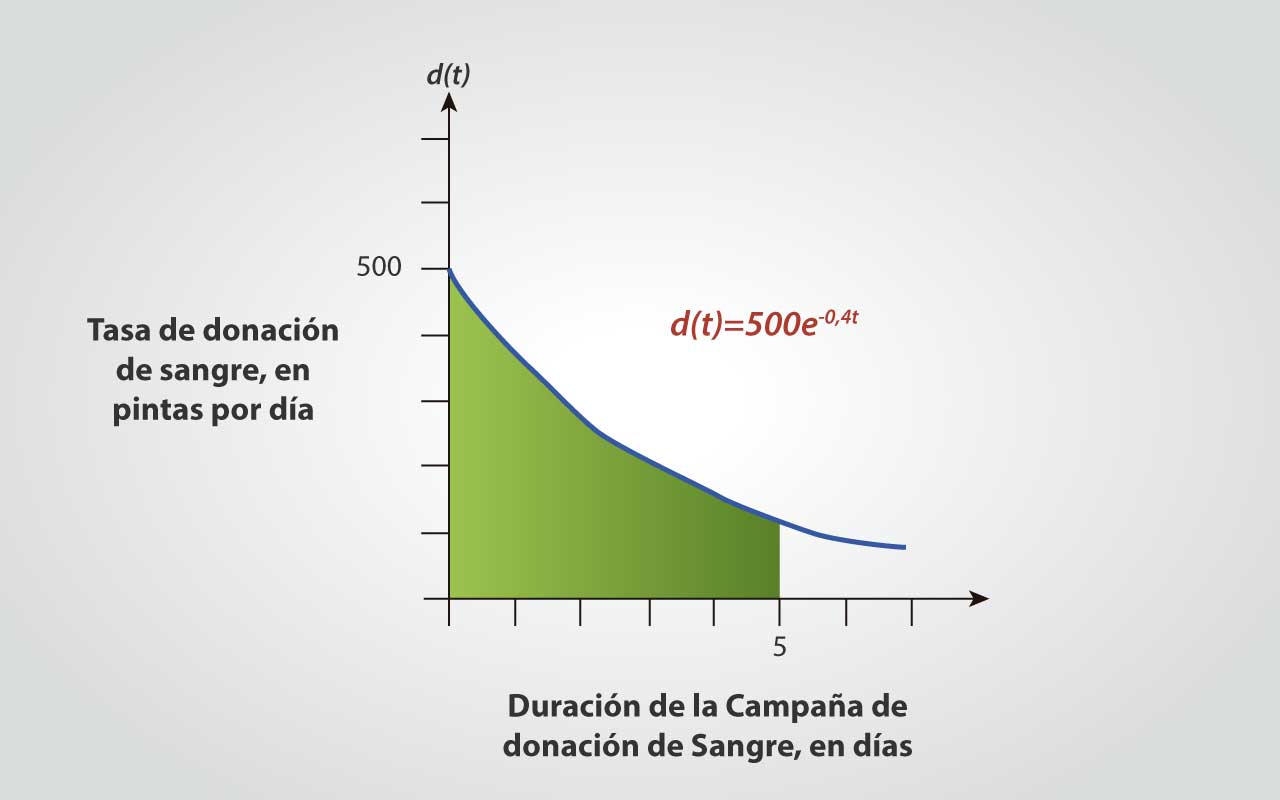
El hospital alcanzará su meta cuando:

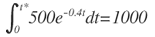
Para dejar la integral inmediata, se sabe que 500= -1250(-0.4), por lo tanto se puede escribir la expresión como:

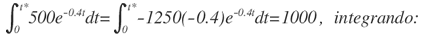
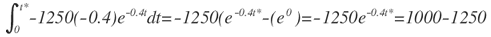
Es decir que:

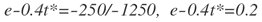
Evaluando el logaritmo natural: ln(e-0.4t*)=ln(0.2), se obtiene: -t*=-1.6094/-0.4.es decir que t*=4.023 días. Es decir la meta de las 1000 pintas se lograría en 4 días aproximadamente.

Ejemplo 5: Energía nuclear

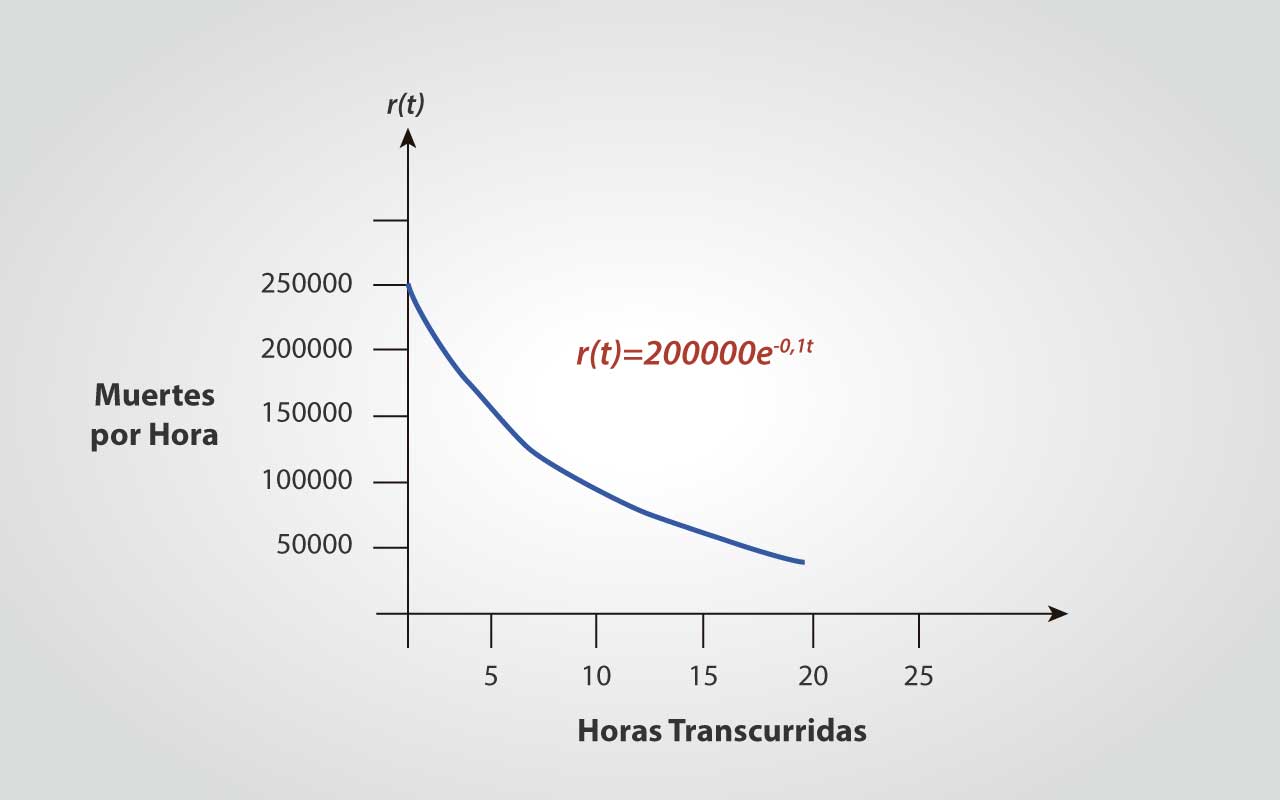
Una compañía eléctrica ha propuesto construir una planta de energía nuclear en las afueras de una gran área metropolitana. Como cabe suponer, la opinión pública está dividida al respecto y se han suscitado acaloradas discusiones. Un grupo que se opone a la construcción de la planta ha ofrecido algunos datos discutibles sobre las consecuencias de un accidente catastrófico que pudiera ocurrir en la planta. El grupo estima que la tasa a que se producirían las muertes en la zona metropolitana por precipitación radioactiva se describe con la función:

Donde r(t) representa la tasa de fallecimientos por hora y t representa el tiempo transcurrido desde el accidente, medido en horas.
Nota: Aunque la controversia en este ejemplo es muy real, los datos son ficticios.

Figura 5. Representación gráfica de tasa de fallecimientos por hora.

La población del área metropolitana es de 1.5 millones de personas.

1. Determine el número esperado de muertos 1 hora después de un gran accidente.
2. ¿Cuánto tardarán todos los habitantes de esta zona en sucumbir ante los efectos de la radioactividad?

a. La figura número 5 ofrece una gráfica de r. El área debajo de esta función entre dos puntos cualesquiera t₁ y t₂ es una medida del número esperado de fallecimientos durante ese intervalo de tiempo. Así pues, el número de muertes esperadas en la primera hora se calcularía como:

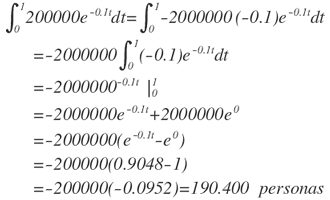
b. Por terrible que parezca, la población entera sucumbirá al cabo de t* horas, donde:

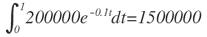
o cuando:

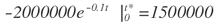
Despejando t* se obtiene:

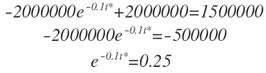
Si se calcula el logaritmo natural en ambos lados de la ecuación:

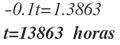
[1] Duarte, G. A. (2013). Aplicaciones de la integral. Bogotá.