Ejemplo de aplicación de los multiplicadores de Lagrange
Maximice: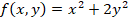 
, sujeto a: 
.
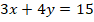Solución
Tomando la segunda opción y observando que: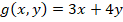 
, se calculan las derivadas parciales de la función 
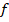y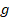 
:
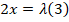
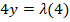
Dividiendo ambas ecuaciones (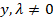
) se tiene que:
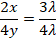
Y tras simplificar se obtiene la ecuación:
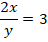
O su equivalente: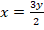 
, que es una expresión que se puede sustituir en la restricción:
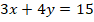
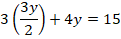
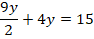
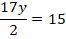
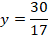
La cual se reemplaza en: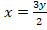
, que da como resultado: 
.
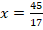Así pues, el óptimo de la función está en: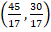 
.