Ejemplo de aplicación de una matriz hessiana
Suponga la función: 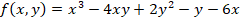 .
.
Las derivadas de cada una de las variables corresponden a:
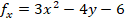
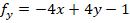
Que igualadas a cero corresponden a un sistema no lineal. Usualmente debería emplearse el método de sustitución, pero en este caso basta con sumar las dos ecuaciones para obtener:
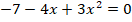
Cuyas soluciones están dadas por:
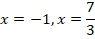
Esto significa que existen dos puntos críticos, uno para cada valor de 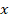 , que deben sustituirse en cualquier ecuación (la más sencilla en este caso es:
, que deben sustituirse en cualquier ecuación (la más sencilla en este caso es: 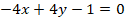 ).
).
Los puntos críticos corresponden a: 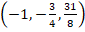 y
y 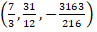 .
.
Para clasificar estos puntos críticos es necesario determinar la matriz hessiana:
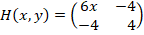
Su determinante corresponde a:
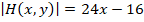
Cada punto crítico se reemplaza en el determinante para determinar clasificación:
Para 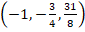 , el determinante corresponde a:
, el determinante corresponde a:
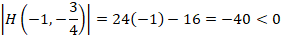
Como el determinante es negativo se afirma que: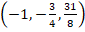 es un punto de silla.
es un punto de silla.
Para 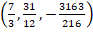 , el determinante queda:
, el determinante queda:
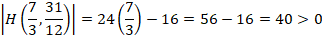
Dado que el determinante es positivo, se hace obligatorio examinar el signo de 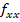 o de
o de 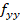 . La segunda derivada de
. La segunda derivada de 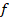 con respecto de
con respecto de 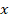 es:
es:
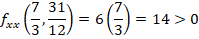
Por lo tanto, como el valor resultante es positivo, así como 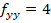 , se afirma entonces que el punto
, se afirma entonces que el punto 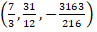 es un mínimo local.
es un mínimo local.
