Ejemplo de optimización sin restricción
Ejercicio
Determine los valores críticos para la función: 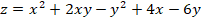 .
.
Solución
Primero se deben calcular las derivadas parciales con respecto de las variables de la función:
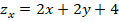
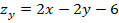
Luego se igualan a cero para resolver el sistema de ecuaciones:
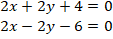
Es importante tener presente que si el sistema es lineal, los métodos usuales como eliminación, sustitución e igualación, serán los más adecuados. En este caso, el método de eliminación es el más eficiente, pues al sumar las dos ecuaciones se obtiene:
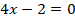
De lo que se deduce que: 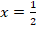 .
.
Sustituyendo el valor de 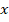 en la primera ecuación, se obtiene que:
en la primera ecuación, se obtiene que:
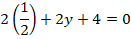
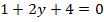
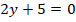
Por lo que se obtiene que: 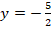 .
.
Entonces, los valores críticos de la función corresponden a: 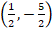 .
.
Al evaluar los valores críticos en la función se obtiene:
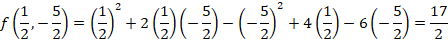
El punto del espacio: 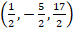 corresponde al punto crítico de la función.
corresponde al punto crítico de la función.
Tras este cálculo surge un nuevo interrogante, ¿cuál es la clasificación del punto?
Puede ser un máximo o mínimo relativo, pero también puede ser un punto de silla o inflexión de la función (donde la función presenta un cambio de concavidad). Se presenta ahora la definición de la matriz hessiana y su determinante (también llamado hessiano) para su clasificación.
