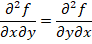Definición
Suponga una función en dos variables: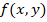 
, con derivadas parciales: 
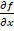y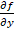 
. Las derivadas parciales de segundo orden corresponden a las derivadas parciales de las derivadas parciales de primer orden. Las derivadas parciales de la derivada con respecto de 
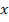, se denotan por:
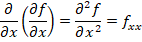
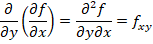
Y las derivadas parciales de la derivada con respecto de
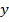, se denotan por: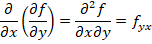
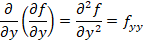
Las derivadas de segundo orden que se obtienen derivando con respecto de variables diferentes, se llaman derivadas de segundo orden mixtas, y cuando la función es continua se satisface que:
