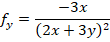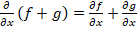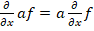Definición de las derivadas parciales
Para complementar el concepto de derivadas parciales, a continuación se presenta la definición de derivada parcial para una función de dos variables, pero que se puede hacer extensible para n variables.
Dada una función: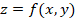 
, se define la derivada parcial de 
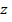respecto de 
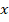por:
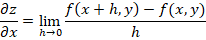
Siempre que el límite exista, también se denotará mediante:
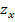o 
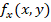.Se observa entonces que la variable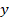 
se comporta como constante y que las propiedades de linealidad se mantienen debido a que es un límite. Estas propiedades son:
La definición de la derivada parcial para y es análoga, con la diferencia de que el incremento está en la variable y, lo que supone que la variable x se comporta como constante, esto es:
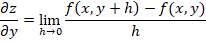
Debe observarse que existe una diferencia substancial en el trato que se le da a las constantes si multiplican o dividen a una función o a las constantes como funciones constantes.
Ejemplo 1
Las derivadas parciales de la función: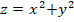 
, respecto a cada variable son:
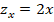
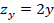
Note que al derivar con respecto de 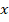, el término 
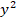se comporta como una función constante y su derivada es cero. Lo mismo ocurre al derivar con respecto de 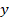, pues en este caso el término 
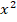es una función constante y por lo tanto su derivada es cero.
Ejemplo 2
Si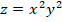 
, sus derivadas parciales son:
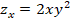
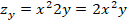
En este caso se observa una diferencia en el trato o la diferencia que se presenta cuando existen términos con combinaciones de y y. En este caso, y2 no varía al momento de derivar con respecto de x, pues es una constante que multiplica a la función x2.
En las derivadas parciales se conservan las mismas derivadas de funciones tradicionales, como la regla del producto, el cociente y regla de la cadena.
Ejemplo 3
Si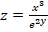 
, sus derivadas parciales son:
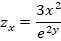
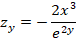
En este caso se puede observar que la derivada con respecto de x en el denominador, el término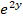 
, permaneció sin variaciones, pues era una constante que estaba dividiendo a la función 
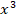. Sin embargo, en la derivada con respecto de y tuvo un tratamiento diferente porque no es posible derivar libremente en el denominador, por lo que se recomienda reescribir la función z como:
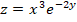
En donde 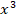queda sin cambios, pero se debe recordar que la derivada con respecto de y de 
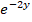debe hacerse por regla de la cadena, esto es derivar la exponencial, la cual es la misma, y multiplicar por la derivada del exponente:
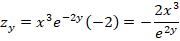
Ejemplo 4
Suponga que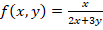 
, entonces ¿cuáles son las derivadas parciales con respecto de cada variable?
Solución
Se aplica la regla del cociente para x, pues existe x en el numerador y en el denominador:
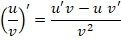
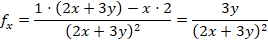
No es necesario aplicar la regla del cociente para calcular la derivada con respecto de y, pues solo se encuentra en el denominador. Para este proceso se puede reescribir la función así:
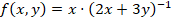
De esta forma se puede derivar por regla de la cadena:
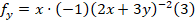
Lo que equivale a:
