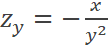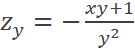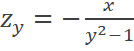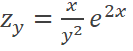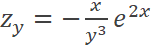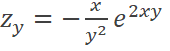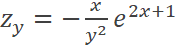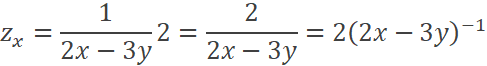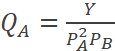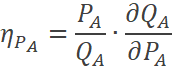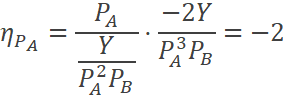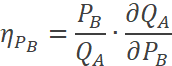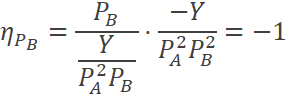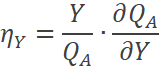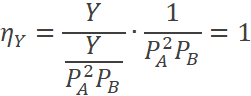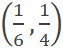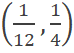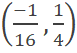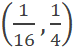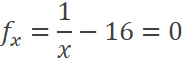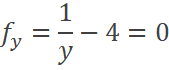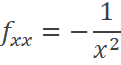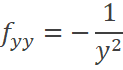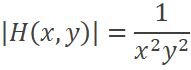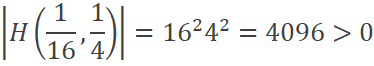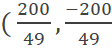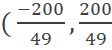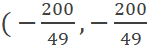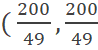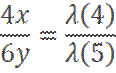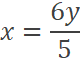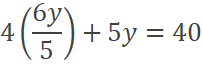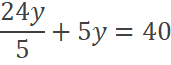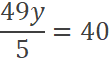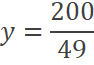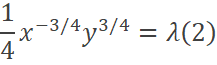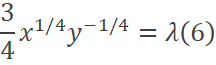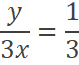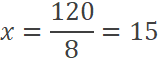SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			1	PANTALLA ASOCIADA	3	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Suponga una función de producción: . Calcule:  y , y analice los resultados. A.  y B.  y . C. y . D. y .
CLAVE			A
RETROALIMENTACIÓN			Se puede concluir que cuando se triplican los factores productivos, la producción también se triplica.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			2	PANTALLA ASOCIADA	3	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Calcule la derivada parcial  de primer orden para la función: . A. . B. . C.. D..
CLAVE			A
RETROALIMENTACIÓN			Si , entonces:   ; .

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			3	PANTALLA ASOCIADA	3	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Calcule las derivadas parciales de primer orden para la función: . A. . B. . C.. D..
CLAVE			D
RETROALIMENTACIÓN			Si , entonces:  (aplicando regla del producto), entonces: (no se aplica producto porque  es contante al derivar respecto de y).

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			4	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Calcule las derivadas de segundo orden:  y  para la función: . A. . B. . C.. D..
CLAVE			A
RETROALIMENTACIÓN			Si , la derivada parcial respecto de , aplicando regla de la cadena, corresponde a: A partir de aquí se calculan las derivadas:  y  o su equivalente: . Del mismo modo, la derivada de respecto de  corresponde a: . A partir de esta derivada se calculan las derivadas:  y  o su equivalente: . Note que: .

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			5	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Calcule las derivadas de segundo orden   para la función A. B. C. D.
CLAVE			A
RETROALIMENTACIÓN			Si , se obtiene: Mientras que las derivadas provenientes de la derivada con respecto de  son:

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			6	PANTALLA ASOCIADA	4	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Determine las elasticidades: precio, cruzada e ingreso de la demanda, para:  con niveles de precios y rentas dados por usted, y diga si  es una demanda unitaria. A. Para algunos valores. B. Solo para valores mayores que cero. C.Solo para valores menores que cero. D.No es una demanda unitaria.
CLAVE			B
RETROALIMENTACIÓN			En algunas funciones de demanda, sin importar los niveles de precios y renta, las elasticidades son las mismas, como en este caso. Independientemente de los valores elegidos, las elasticidades son: Se concluye entonces que para la elasticidad «precio de la demanda» es una demanda elástica, mientras que para las elasticidades «cruzada» e «ingreso» es una demanda unitaria.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			7	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Determine y clasifique los puntos críticos de la función: . A. (-2, 2) máximo. B. (2, -2) máximo. C.(-2, 2) mínimo. D.(-2, 2) mínimo.
CLAVE			D
RETROALIMENTACIÓN			Suponiendo que: , las derivadas parciales corresponden a: Que igualando a cero y resolviendo el sistema por el método de eliminación (multiplicando la primera ecuación por -1) se obtiene: Y por lo tanto: , luego se tienen valores críticos: . El determinante de la matriz hessiana corresponde a: Dado que: , se puede concluir que el punto crítico es un mínimo.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	3	PREGUNTA #			8	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Determine y clasifique los puntos críticos de la función: . A.  máximo. B.  máximo. C. mínimo. D. máximo.
CLAVE			D
RETROALIMENTACIÓN			Si , las derivadas parciales de primer orden corresponden a: Igualando a cero cada derivada y despejando, se tienen los valores críticos: , y las derivadas parciales de segundo orden corresponden a: Por tanto, el determinante de la matriz hessiana es: Evaluando en: , se obtiene: Y como: , el punto crítico es un máximo relativo.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			9	PANTALLA ASOCIADA	6	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Determine el máximo de: , sujeto a: . A. ). B. ). C.). D.).
CLAVE			D
RETROALIMENTACIÓN			Se busca hallar el máximo de: , sujeto a: , entonces: De lo que se obtiene que: Despejando  se obtiene: Y reemplazando en la restricción: Por lo tanto: .

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	4	PREGUNTA #			10	PANTALLA ASOCIADA	6	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Determine la utilidad máxima del consumidor, cuando este tiene una función de utilidad definida por:  sujeta a la restricción presupuestal: . A. . B. . C.. D..
CLAVE			C
RETROALIMENTACIÓN			Suponiendo que se desea maximizar:  sujeta a la restricción presupuestal: , se procede a calcular las derivadas parciales de la utilidad e igualarlas a las derivadas parciales de la restricción que coinciden con los precios unitarios de los bienes: Entonces: Dividiendo ambas ecuaciones: Reemplazando luego en la restricción presupuestal: Por lo tanto, los niveles de consumo que generan la máxima utilidad de consumo se encuentran en:  y la máxima utilidad es: