Segundo teorema de las funciones crecientes y decrecientes
- Si
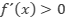para cada 
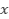en algún intervalo 
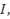entonces 
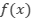es creciente en el intervalo. - Si
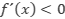para cada 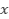en algún intervalo 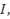entonces 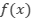es decreciente en el intervalo. - Si
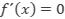para cada 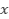en algún intervalo 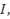entonces 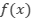es constante en el intervalo.
Suponga que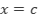 
es un punto crítico de 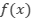, entonces:
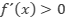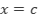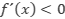- Si a la izquierda de y a la derecha de 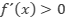, entonces 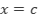es un máximo relativo.
- Si 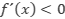a la izquierda de 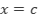y 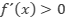a la derecha de 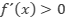, entonces 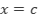es un máximo relativo.
- Si
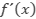es la misma en ambos lados de 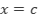, entonces 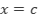no es ni máximo relativo ni mínimo relativo.