Teorema de máximos y mínimos
- f(x) tiene un máximo absoluto o global en x=c si f(x)≤f(c) para todo x en el dominio definido.
- f(x) tiene un máximo relativo o local en x=c si f(x)≤f(c) para todo x en algún intervalo abierto alrededor de x=c.
- f(x) tiene un mínimo absoluto o global en x=c si f(x)≥f(c) para todo x en el dominio definido.
- f(x) tiene un mínimo relativo o local en x=c si f(x)≥f(c) para todo x en algún intervalo abierto alrededor de x=c.
Tenga en cuenta que el «intervalo abierto alrededor x=c» quiere decir que se puede encontrar algún intervalo (a,b), de tal manera que c está contenido en algún lugar dentro del intervalo y no coincidirá con ninguno de los puntos limite.
De igual manera, recuerde que de manera general se les denomina «puntos máximos y mínimos de una función» a los extremos de dicha función; «extremos relativos» a los máximos y mínimos relativos, y «extremos absolutos» a los mínimos y máximos absolutos.
Por otra parte, se entiende como «dominio a trabajar» aquel rango de las x con el que se trabaja en una determinada función. Puede que existan otros valores de x que puedan ser tomados en la función, pero por algún motivo fueron excluidos.
En cuanto a la diferencia sutil entre lo absoluto y lo relativo, en la definición anterior, se tiene un máximo o mínimo absoluto de x=c, al punto que proporciona a f(c) el valor más alto o más bajo que la función tomará siempre en el dominio a trabajar.
Un máximo o mínimo relativo es ligeramente diferente, pues todo lo que necesita un punto para ser un máximo relativo o un mínimo relativo es que dicho punto sea un máximo o un mínimo en un intervalo de las x alrededor de x=c. Pueden existir valores mayores o menores de la función en algún otro lugar, pero siempre debe ser relativo a x=c o local a x=c. En este caso, f(c) es mayor o menor que todos los otros valores de la función que están cerca a él.
Dónde buscar máximos y mínimos

|
Para saber si existe un máximo o un mínimo en un determinado punto no se debe buscar en los puntos extremos del dominio, pues esta situación solo puede ocurrir al interior del dominio. |
Por lo general, es más fácil tener una idea de las definiciones mediante la adopción de una representación gráfica como la siguiente:
Figura 1.
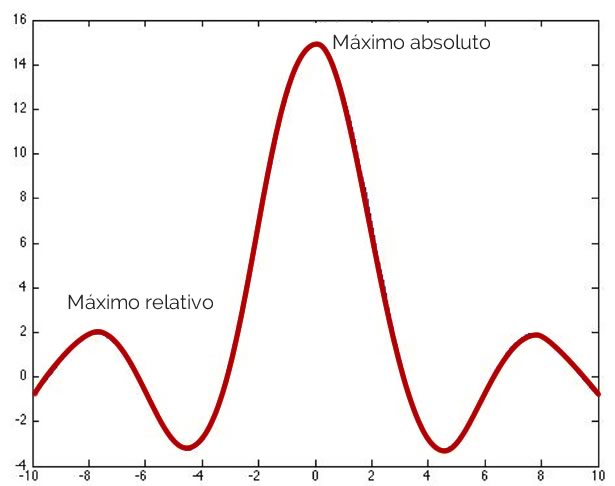
(Para ampliar la imagen haga clic sobre ella)
Ejemplo
Identificar los extremos absolutos y los extremos relativos de la función: f(x)=x2 en [-1,2].
Solución
Figura 1.

(Para ampliar la imagen haga clic sobre ella)
Tenga en cuenta que se utilizaron los puntos inicial y final para mostrar que la gráfica termina en estos puntos, lo que permite identificar los extremos de la gráfica. En este caso parece que se tiene un mínimo relativo y absoluto en x=0 y un máximo absoluto en x=2. Tenga en cuenta que x=-1 no es un máximo relativo ya que es el punto final del intervalo, es decir que esta función no tiene máximos relativos.
Recapitulación
Mediante este ejemplo se demostró el hecho de que puede haber extremos un infinito número de veces en una sola gráfica. A continuación se trabajará con ejemplos en los que se pueden ver los extremos absolutos de forma mas clara. Antes de proseguir con ellos, note que las gráficas de las anteriores funciones eran continuas, estaban definidas en intervalos cerrados y tenían un solo máximo o mínimo absoluto. Estas observaciones convergen en el siguiente teorema.
Por lo tanto, si se tiene una función continua en un intervalo [a,b], entonces está garantizado que se puede tener a la vez un máximo absoluto y un mínimo absoluto en la misma función. El teorema no dice donde ocurrirá o si ocurrirá más de una vez, pero al menos dice que sí existen en alguna parte. A veces, todo lo que se necesita es saber si existen.
