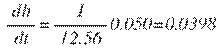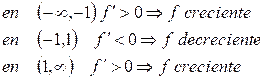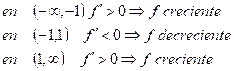SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

1

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Si se vierte agua en un estanque cilíndrico de dos metros de radio basal y cuatro metros de altura, a razón de 50 litros por minuto, ¿con qué rapidez ascenderá el nivel del agua?

 

A.    0.039 litros por minuto.

B.    0.12 litros por minuto.

C.   12 litros por minuto.

D.   36 litros por minuto.

CLAVE

A

RETROALIMENTACIÓN

Si se llama h a la altura del nivel de líquido en cualquier momento, se puede expresar el volumen del contenido en función de h, de la forma: V=π r2h, así que despejando h se tiene:

 

h=, en donde π y r son constantes, luego al derivar resulta:  . Pero debido a que ingresa agua a razón de 50 litros por minuto (dV/dt), entonces:

 

../../../../Desktop/daum_equation_1520427377622.png[UdMO1] 

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

2

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Utilice el criterio de la segunda derivada para encontrar los extremos de la función:

f(x)=x3–6x2–15x

 

A.   En x1=-1 se tiene un máximo de f, y en x2=-5 se tiene un mínimo de f.

B.   En x1=1 se tiene un máximo de f, y en x2=5 se tiene un mínimo de f.

C.   En x1=-1 se tiene un máximo de f, y en x2=5 se tiene un mínimo de f.

D.   En x1=1 se tiene un máximo de f, y en x2=-5 se tiene un mínimo de f.

E.     

CLAVE

C

RETROALIMENTACIÓN

f´(x)=3x2–12x–15=0 Þ puntos críticos:

 

x1=-1 y x2=5

 

f´´(x)=6x–12     

Þ f´´(-1)=-18<0 Þ en x1=-1 se tiene un máximo de f.

 

Þ f´´(5)=18>0 Þ en x2=5 se tiene un mínimo de f.

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

3

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Un trozo de alambre de 20 cm de largo se corta en dos partes; una parte se dobla para formar un cuadrado y con la otra se forma una circunferencia. ¿Dónde se deberá hacer el corte para que la suma de las áreas del cuadrado y del círculo sea un mínimo?

 

A.     x=11.2 cm.

B.     x=28 cm.

C.    x=12 cm.

D.    x=32 cm.

CLAVE

A

RETROALIMENTACIÓN

Con el primer segmento se construye el cuadrado cuyo lado medirá x/4 y con el resto se construye la circunferencia cuyo radio medirá: 2πr=L–x Þ .

 

Por lo tanto, las áreas medirán: Acuadrado =  y Acírculo =

 

Entonces, el área total será: Atotal =  +

 

La primera derivada del área total respecto de x resulta:

 

Igualando a cero y despejando el valor de x queda:

 

La segunda derivada del área total respecto de x queda:

 

Lo cual indica que x es positiva y en consecuencia el valor del área es un mínimo. Al remplazar el valor de la longitud del alambre (20 cm) en x, se obtiene que x=11.2 cm.

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

4

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

El mínimo relativo de la función: , se encuentra en:

 

A.   .

B.   .

C.   .

D.   No tiene.

CLAVE

A

RETROALIMENTACIÓN

, al estudiar el signo de la derivada se obtiene:

 

 

Como en  la función pasa de ser decreciente a creciente,  tiene un mínimo relativo en  que vale: .

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

5

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

El máximo relativo de la función: , se encuentra en:

 

A.   .

B.   .

C.   .

D.   No tiene.

CLAVE

C

RETROALIMENTACIÓN

, al estudiar el signo de la derivada se obtiene:

 

 

Como la función en  pasa de creciente a decreciente, tiene en  un Máximo relativo que vale: ().

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

6

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Una cadena de supermercados estima que sus ingresos anuales en pesos se determinan por medio de la función: , mientras que sus gastos se determinan por medio de la función: , donde  representa la cantidad de unidades vendidas. A partir de esta información, determine la función que define el beneficio anual en pesos y elija la cantidad de unidades que deben ser vendidas para que el beneficio sea máximo.

 

A.   70 unidades.

B.   750 unidades.

C.   7500 unidades.

D.   No importa cuántas unidades venda, el beneficio es el mismo.

CLAVE

B

RETROALIMENTACIÓN

Si se requiere conocer el máximo de la función: , se debe calcular:

 

 

Y calcular los puntos críticos:

 

 

Ahora se comprueba el criterio del signo de la segunda derivada, que es un máximo:

 

 

Entonces para obtener el máximo beneficio se han de vender  unidades.

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

7

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Una cadena de supermercados estima que sus ingresos anuales en pesos se determinan mediante la función: , mientras que sus gastos se determinan por medio de la función: , donde representa la cantidad de unidades vendidas. A partir de esta información determine la función que define el beneficio anual en pesos y elija la opción que indique el beneficio máximo.

 

A.   .

B.   .

C.   .

D.   .

CLAVE

A

RETROALIMENTACIÓN

Para calcular el beneficio máximo se debe evaluar la función del beneficio en .

 

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

8

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Halle los máximos, los mínimos y los puntos de inflexión de la función: , para determinar dónde es cóncava:

 

A.   Es cóncava en (1, +5).

B.   Es cóncava en (1, -1).

C.   Es cóncava en (1, +5).

D.   Es cóncava en (1, +).

CLAVE

D

RETROALIMENTACIÓN

f'(x)=2(x-2)·(x+1)+(x-2)2=(x-2)·[2(x+1)+x-2]

 

=(x-2)·(2x+2+x-2)=3x(x-2)=3x2-6x

 

Signo de f'(x):

 

 

f(x) es creciente en: (-, 0)(2, +); es decreciente en: (0, 2); tiene un máximo en: (0, 4) y un mínimo en (2, 0).

 

Segunda derivada:

 

f''(x)=6x-6

 

f''(x)=06x-6=0x=1

 

Signo de f''(x):

 

 

f(x) es cóncava hacia abajo en (-, 1); es cóncava hacia arriba en (1, +) y tiene un punto de inflexión en: (1, 2).

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

9

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Un heladero ha comprobado que a un precio de 50 céntimos de euro por unidad vende una media de 200 helados diarios, pero por cada céntimo que aumenta el precio vende dos helados menos por día. Si el valor de cada helado es de 40 céntimos, ¿a cuál precio de venta el heladero obtendrá el máximo beneficio?

 

A.   60 euros.

B.   75.80 euros.

C.   58.50 euros.

D.   60.50 euros.

CLAVE

D

RETROALIMENTACIÓN

En este caso se debe llamar x al número de céntimos en los que aumenta el precio. Así, cada helado costará  50+x céntimos, y venderá 200-2x helados diarios. Por tanto, por la venta de los helados obtendrá los siguientes ingresos:

 

I(x)=(50+x)·(200 - 2x)

 

Pero tiene unos gastos de: G(x)=(200-2x)·40

 

Luego, el beneficio será de:

 

B(x)=I(x)-G(x)=(50+x)(200-2x)-(200-2x)·40=(200-2x)(50+x-40)

=(200-2x)(x+10)

=-2x2+180x+2000

 

Se halla x para que el beneficio sea máximo:

 

B'(x)=-4x+180

B'(x)=0-4x+180=0x=45

B''(x)=-4; B''(45)<0 en: x=45 hay un máximo.

 

Por lo tanto, el heladero obtendrá el máximo beneficio vendiendo cada helado a 50+45 céntimos de euro. O sea, el beneficio sería de  B(45)=6050 céntimos; es decir, 60.50 euros.

 

SEMESTRE

2

MATERIA

Matemáticas II

UNIDAD

3

PREGUNTA #

10

PANTALLA ASOCIADA

 

TIPO PREGUNTA

 

CUERPO DE LA PREGUNTA

Halle los intervalos donde decrece la función:

 

../../../../Desktop/daum_equation_1520435279294.png[UdMO2] 

 

A.   .

B.   .

C.   .

D.   .

CLAVE

A

RETROALIMENTACIÓN

Dominio = -{1}

 

Derivada:

 

 

 

Signo de f'(x).

 

 

f(x) es creciente en: (, 0)(2, ); es decreciente en: (0, 1)(1, 2) y tiene un máximo en: (0, -2) y un mínimo en: (2, 2).

 

 [UdMO1]\frac { dh }{ dt } =\frac { 1 }{ 12.56 } 0.050=0.0398

 [UdMO2]f\left( x \right) =\frac { { x }^{ 2 }-2x+2 }{ x-1 }