Funciones implícitas y explícitas

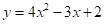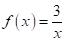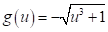Funciones como estas están definidas por expresiones en las que se identifican las variables dependiente e independiente de manera clara. En el caso de las funciones expuestas, las variables dependientes son: y, f(x) y g(u), mientras que las independientes son: x y u.

Al derivar estas funciones, el lado izquierdo de cada una de ellas toma la forma: y', f'(x) y g'(u) respectivamente, mientras que el lado derecho toma la forma de una expresión hallada mediante las reglas anteriormente estudiadas, en este caso: 8x-3, -3/x2 y -3u²/2√u³+1 respectivamente.

No sucede lo mismo con ecuaciones o funciones como: 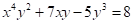, donde:

1. No se identifica de manera sencilla cuál variable es la dependiente y cuál, la independiente.
2. No es posible —o en caso de ser posible, resulta muy dispendioso— despejar o mostrar la expresión de forma explícita.