Cálculo de una derivada
Figura 1.
(Para ampliar la imagen haga clic sobre ella)
Sea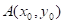 
un punto fijo, y 
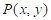un punto variable en la curva 
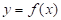, como se muestra en la figura. Entonces, la pendiente se define como:
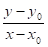o 
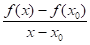
Cuando el punto P se mueve cada vez más cerca de A a través de la curva y=f(x), es decir,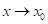
, la línea AP resulta ser la línea tangente de la curva en el punto A. Por tanto, la pendiente de la línea tangente en el punto A es igual a:
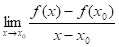
Este término, está definido como la derivada de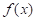 
en 
, y usualmente se denota como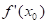 
.
En resumen, el cálculo de la pendiente de la recta tangente o la tasa de cambio instantánea de una función, y la velocidad instantánea de un objeto en x=a requiere calcular el limite:
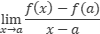
Entones, definimos un cambio de notación:
