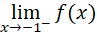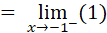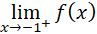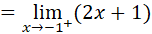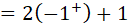Ejemplos de la aplicación del concepto de continuidad
Ejemplo 1
Demostrar que 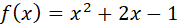 , es continua en
, es continua en 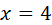 .
.
Para demostrar esto, se deben verificar las tres condiciones para que una función sea continua en un punto.
Condición 1
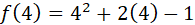
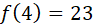
Por lo tanto existe. Si no existiera, la función sería discontinua y terminaría el análisis.
Condición 2
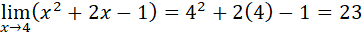
Entonces: 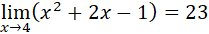
Es decir que sí existe.
Condición 3
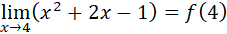
Se evidencia que la condición 1 y la condición 2 son iguales.
Por lo tanto la función 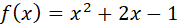 es continua en
es continua en 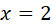 .
.
Ejemplo 2
Analizar la continuidad de la siguiente función, definida a trozos o a pedazos, en el punto 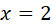 :
:
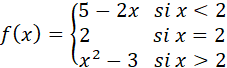
Para comenzar, se deben aplicar las condiciones de la definición de continuidad.
Condición 1
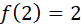 ,de acuerdo con la segunda condición de la función.
,de acuerdo con la segunda condición de la función.
Condición 2
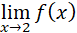 ,se debe calcular el límite por la izquierda y por la derecha.
,se debe calcular el límite por la izquierda y por la derecha.
| Por la izquierda | Por la derecha |
|
|
|
Por lo tanto, 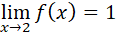 sí existe, pues los resultados son iguales por la izquierda y por la derecha.
sí existe, pues los resultados son iguales por la izquierda y por la derecha.
Condición 3
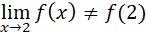 , por lo tanto la función
, por lo tanto la función 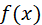 es discontinua en x=2.
es discontinua en x=2.
Aunque este ejercicio se resolvió sin graficar la función, el siguiente ejemplo tendrá una gráfica para demostrar la importancia de graficar.
Ejemplo 3
Analizar la continuidad de la siguiente función, definida a trozos o por secciones, en el punto x=2.
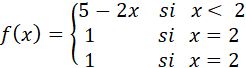
La gráfica correspondiente a esta función se obtiene dando valores a x que cumplan con la primera condición, o sea valores entre -∞ y 2. Esto arroja la línea recta 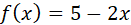 .
.
El segundo trozo o sección se obtiene dando a x el único valor que debe cumplir: x=2, lo cual arroja un punto en el que la función vale uno. Esto da como resultado:
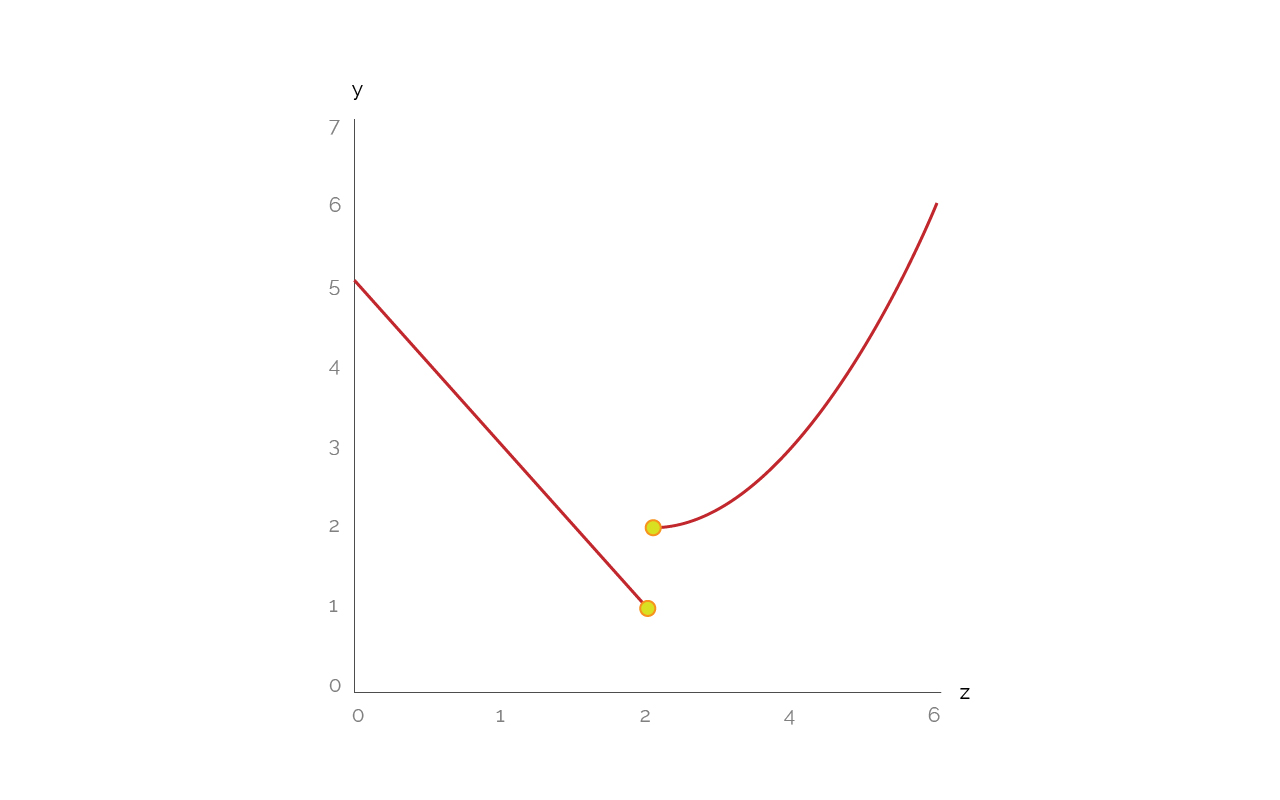
Tras graficar, se aplican las condiciones para verificar la continuidad.
Condición 1
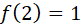 , reemplazando.
, reemplazando.
Condición 2
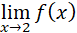 ,se debe calcular el límite por la izquierda y por la derecha.
,se debe calcular el límite por la izquierda y por la derecha.
| Por la izquierda | Por la derecha |
|
|
|
Por lo tanto, 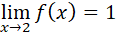 sí existe, pues los resultados son iguales por la izquierda y por la derecha.
sí existe, pues los resultados son iguales por la izquierda y por la derecha.
Condición 3
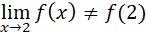 , por lo tanto la función
, por lo tanto la función 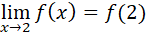 es discontinua en x=2.
es discontinua en x=2.
Ejemplo 4
Encuentre los puntos de discontinuidad de la siguiente función:
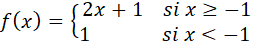
Las expresiones 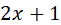 y 1 que conforman la función son polinomios, por lo tanto son continuas de acuerdo con la cuarta propiedad de las funciones continuas. El otro valor a estudiar es
y 1 que conforman la función son polinomios, por lo tanto son continuas de acuerdo con la cuarta propiedad de las funciones continuas. El otro valor a estudiar es  , en el que puede haber separaciones entre las gráficas, generando discontinuidad.
, en el que puede haber separaciones entre las gráficas, generando discontinuidad.
Al aplicar las condiciones de la continuidad se obtiene:
| 1 | 2 |
|
|
|
El límite no existe, por lo tanto la función f es discontinua en x=-1.
Ejemplo 5
Encontrar los puntos de discontinuidad de la siguiente función racional:
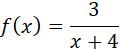
En el denominador se tiene que x+4=0 cuando x=-4, por lo tanto la función es discontinua en 4.

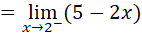 , por cumplir la primera condición, que indica los valores por la izquierda de dos, es decir, valores menores que dos.
, por cumplir la primera condición, que indica los valores por la izquierda de dos, es decir, valores menores que dos. , reemplazando.
, reemplazando. 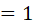 , resolviendo.
, resolviendo.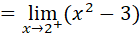 ,por cumplir con la tercera condición, que indica los valores por la derecha de dos, es decir, valores mayores que dos.
,por cumplir con la tercera condición, que indica los valores por la derecha de dos, es decir, valores mayores que dos.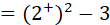 , reemplazando.
, reemplazando. 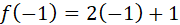 , reemplazando.
, reemplazando.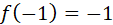 , resolviendo.
, resolviendo.