Actividad de aprendizaje
A continuación se demostrará la primera propiedad de las funciones continuas. Preste atención al desarrollo de la demostración, pues al final se le pedirá que usted demuestre las otras cuatro propiedades.
Demostración de la propiedad 1
Si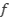 
es continua en 
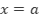, entonces 
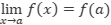, por definición de continuidad.
Si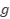 
es continua en 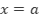, entonces 
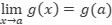, por definición de continuidad.
Se tiene entonces:
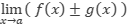
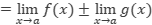, por la propiedad de los límites.
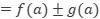, debido a que 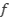y 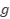son continuas. Entonces:
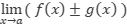
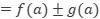
Por lo tanto la función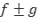 
es continua en .
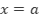La demostración de las otras propiedades se hace de manera semejante a esta, así que desarrolle las cuatro demostraciones faltantes y socialice el resultado con el tutor de la asignatura.