Límites al infinito
En la siguiente figura se evidencia que en la medida que 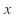 aumenta su valor, la función
aumenta su valor, la función 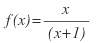 adquiere valores cada vez más cercanos a uno, por lo cual podemos decir que
adquiere valores cada vez más cercanos a uno, por lo cual podemos decir que 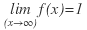 . En este caso, la recta
. En este caso, la recta  es una asíntota horizontal.
es una asíntota horizontal.
Figura 1. Representación de la función 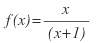
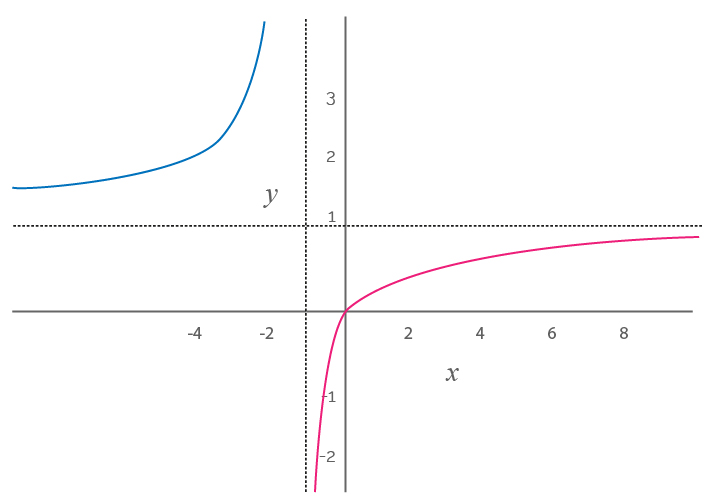
Fuente: Elaboración propia.
(Para ampliar la imagen haga clic sobre ella)
 |
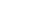 |
| 1 | 0.5000 |
| 15 | 0.9375 |
| 30 | 0.9677 |
| 45 | 0.9783 |
| 60 | 0.9836 |
| 85 | 0.9844 |
| 110 | 0.9910 |
Es importante recordar que la notación  no es un número, sino una forma de decir que
no es un número, sino una forma de decir que 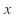 aumenta positivamente sin límite, mientras que la notación
aumenta positivamente sin límite, mientras que la notación 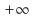 es una forma de indicar que la variable crece de tal manera que no es posible determinar hasta dónde.
es una forma de indicar que la variable crece de tal manera que no es posible determinar hasta dónde.
Operaciones con el símbolo ∞



 , con
, con 


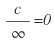 , con
, con 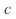 constante
constante
Cabe recordar que las indeterminaciones no significan que el límite no existe, sino que se debe cambiar la expresión algebraica que genera dicha indeterminación para poder eliminarla y obtener así el límite hacia el cual tiende la función.
Recapitulación
Cuando se calculan límites al infinito se busca comprender cómo se comporta una función cuando x toma valores positivos cada vez más grandes, lo cual se nota como:  , y cuando x toma valores negativos cada vez más grandes, lo cual se nota como:
, y cuando x toma valores negativos cada vez más grandes, lo cual se nota como:  .
.
En el cálculo de límites al infinito suelen ocurrir los siguientes casos:
- Los valores de
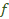 correspondientes a valores de
correspondientes a valores de 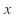 muy grandes, positivos o negativos, tienden a ser también muy grandes (positivos o negativos).
muy grandes, positivos o negativos, tienden a ser también muy grandes (positivos o negativos). - Los valores de
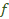 correspondientes a valores de x muy grandes, positivos o negativos, tienden a un número real.
correspondientes a valores de x muy grandes, positivos o negativos, tienden a un número real. - El valor del límite cuando
 puede ser
puede ser , y se nota:
, y se nota:  o
o 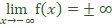 .
. - El valor del límite cuando
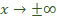 , es
, es 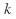 , y se nota:
, y se nota: 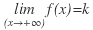 o
o 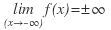 .
.
Por otra parte, cuando se calculan límites infinitos se busca determinar cómo se comporta f cuando  . Al hacer este tipo de cálculos, suele ocurrir el siguiente caso:
. Al hacer este tipo de cálculos, suele ocurrir el siguiente caso:
- El límite cuando
 es
es 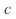 , y se nota:
, y se nota: 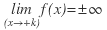 .
.



