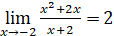Límites y sus propiedades
Al graficar la función 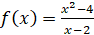 se puede observar que cuando x se acerca a dos, sin llegar a ser dos, los valores de la función se acercan a cuatro. Tal situación se muestra a continuación:
se puede observar que cuando x se acerca a dos, sin llegar a ser dos, los valores de la función se acercan a cuatro. Tal situación se muestra a continuación:
Figura 1. Gráfica de la función 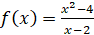
(Para ampliar la imagen haga clic sobre ella)
Tabla 1. Valores de la función 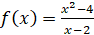
| Valores de x menores que 2 | Valores de x mayores que 2 | ||
| x | f(x) | x | f(x) |
| 1.8 | 3.8 | 2.1 | 4.1 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 | 2.001 | 4.001 |
| 1.999 | 3.99 | 2.0001 | 4.0001 |
Como se puede ver, cuando x se acerca a dos con valores menores que dos, la función se acerca a cuatro; lo mismo sucede cuando x se acerca a dos con valores mayores que dos. Observe que la función nunca toma el valor dos, ya que el numerador y el denominador serían cero y, por lo tanto, la función no estaría definida. En este caso se puede decir que dos no pertenece al dominio.
Teorema
Si x se aproxima a un valor dado a, y f(x) se acerca a un número real L, se dice entonces que L es el límite de la función y=f(x) cuando x tiende a a, y se escribe:
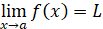
Se debe tener en cuenta que a puede o no estar en el dominio de f, puesto que x nunca va a tomar el valor de a.
Propiedades de los límites
- El límite de una constante es la misma constante.
- El límite de una potencia es la potencia del límite.
- El límite de una suma o resta de funciones es la suma o resta de los límites de las funciones.
- El límite de un producto de funciones es el producto de los límites de las funciones.
- El límite de un cociente de funciones es el cociente de los límites de las funciones.
- El límite del producto de una constante por una función es el producto de la constante por el límite de la función.
- Si el límite de una función existe, este límite es único.
Antes de calcular límites es importante recordar que el límite es único y es un número real. Así mismo, se debe tener en cuenta que si se aplican las propiedades para hallar un límite y no es posible encontrarlo, se establece una indeterminación, en cuyo caso se debe realizar un cambio equivalente de la función original para aplicar nuevamente las propiedades y finalmente encontrar el límite buscado.
Ejemplo
A continuación se muestran algunas expresiones que se pueden presentar en la determinación de los límites: ,
,  y
y 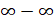 Estas expresiones se denominan indeterminaciones.
Estas expresiones se denominan indeterminaciones.Sea:
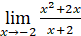
Para resolver este límite, se aplican una a una las propiedades:
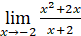
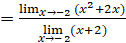 , por la propiedad 5.
, por la propiedad 5.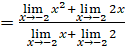 , por la propiedad 3.
, por la propiedad 3.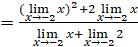 , por las propiedades 2 y 6.
, por las propiedades 2 y 6.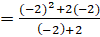 , por las propiedades 1 y 2.
, por las propiedades 1 y 2.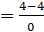 , resolviendo.
, resolviendo.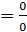 , se tiene una indeterminación.
, se tiene una indeterminación.Para eliminar esta indeterminación se transforma la expresión original de la siguiente manera:
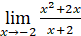
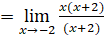 , factorizando.
, factorizando.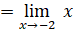 , simplificando.
, simplificando.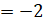 , reemplazando.
, reemplazando.Por lo tanto: