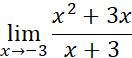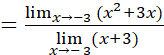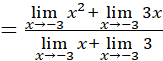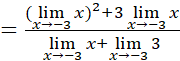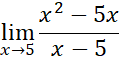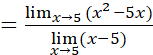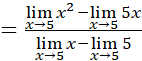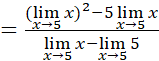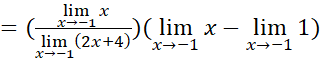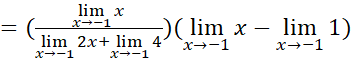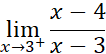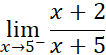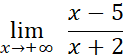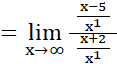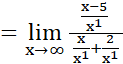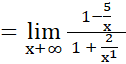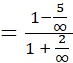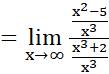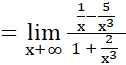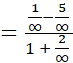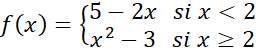SEMESTRE	II	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			1	PANTALLA ASOCIADA	3		TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Resuelva el siguiente límite utilizando las propiedades de los límites: A. 2 B. -3 C. 4 D. -2
CLAVE			B
RETROALIMENTACIÓN			, por P-5. , por P-3. , por P-2 y P-6. , por P-1 y P-2. , es una indeterminación.					Para eliminar la indeterminación se transforma la expresión original así: , factorizando.       , simplificando.

SEMESTRE	II	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			2	PANTALLA ASOCIADA	3		TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Resuelva el siguiente límite utilizando las propiedades de los límites: A. 2 B. -3 C. -5 D. 5
CLAVE			D
RETROALIMENTACIÓN			, por P-5. , por P-3. , por P-2 y P-6. , reemplazando. , es una indeterminación.					Para eliminar la indeterminación se transforma la expresión original así: , factorizando. , simplificando.

SEMESTRE	II	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			3	PANTALLA ASOCIADA	4		TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Halle  en la siguiente función: A. -2 B. 4 C. 2 D. 1/2
CLAVE			A
RETROALIMENTACIÓN			Para hallar el límite se debe hallar primero: . Se reemplazó 3 en el intervalo para el cual x<3:					Luego se calcula:. Se reemplaza 3 en el intervalo para el cual x > 3: Por lo tanto, el límite existe y es: .

SEMESTRE	II	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			4	PANTALLA ASOCIADA	3		TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Resuelva el siguiente límite utilizando las propiedades de los límites: A. -1 B. 0 C. 3 D. -2
CLAVE			B
RETROALIMENTACIÓN			] , por P-4. , por P-5 y P-3. , por P-3.					, por P-1. , reemplazando. , resolviendo.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			5	PANTALLA ASOCIADA	4	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Halle el siguiente límite: A. -5 B. C. 6 D.
CLAVE			D
RETROALIMENTACIÓN			Lo primero que se debe hacer es reemplazar el valor de la variable en la función. , reemplazando  por . , simplificando. , que es negativo porque el numerador es negativo y el denominador es positivo.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			6	PANTALLA ASOCIADA	4	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Halle el límite y seleccione la respuesta correcta: A. -1 B. 0 C. D.
CLAVE			C
RETROALIMENTACIÓN			, reemplazando  por . , simplificando. , que es negativo porque el numerador es positivo y el denominador es negativo.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			7	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Halle el siguiente límite: A. -1 B. 0 C. 1 D. -2
CLAVE			C
RETROALIMENTACIÓN			, dividiendo entre . , distribuyendo. , simplificando. , remplazando  por . , aplicando el límite estudiado. , por lo tanto: 1

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			8	PANTALLA ASOCIADA	5	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Halle el siguiente límite: A. -1 B. 0 C. 1 D. -2
CLAVE			B
RETROALIMENTACIÓN			, dividiendo entre . , distribuyendo. , simplificando. , remplazando  por . , aplicando el límite estudiado.

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			9	PANTALLA ASOCIADA	6	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Analizar la continuidad de la siguiente función definida a trozos o a pedazos, en el punto : A. No es continua en , pues no se cumple ninguna condición de continuidad. B. Sí es continua en , porque se cumplen las tres condiciones de continuidad. C. No es continua en , pues no se cumple la primera condición de continuidad. D. Sí es continua en , pero no en otro punto.
CLAVE			B
RETROALIMENTACIÓN			En este caso se debe comenzar aplicando cada una de las condiciones de la definición de continuidad: 1. , de acuerdo con la segunda condición de la función. 2. , se debe calcular el límite por la izquierda y por la derecha. , por cumplir con la primera condición de la función dada, que indica los valores por la izquierda de 2, es decir, valores menores que 2. , reemplazando. , resolviendo Ahora por la derecha: , por cumplir con la tercera condición de la función dada, que indica los valores por la derecha de 2, es decir, valores mayores que 2. , reemplazando. , por lo tanto: . Sí existe, pues son iguales por izquierda y por derecha. Verificando la última condición: , por lo tanto la función  es continua en .

SEMESTRE	2	MATERIA		Matemáticas II
UNIDAD	1	PREGUNTA #			10	PANTALLA ASOCIADA	6	TIPO PREGUNTA
CUERPO DE LA PREGUNTA			Analizar la continuidad de la siguiente función definida a trozos o a pedazos, en el punto : A. No es continua en , pues no se cumple ninguna condición de continuidad. B. Sí es continua en , porque se cumplen las tres condiciones de continuidad. C. No es continua en , pues no se cumple la primera condición de continuidad. D. Sí es continua en , pero no en otro punto.
CLAVE			B
RETROALIMENTACIÓN			Se debe comenzar aplicando cada una de las condiciones de la definición de continuidad: 1. , de acuerdo con la segunda condición de la función. 2. , se debe calcular el límite por la izquierda y por la derecha. , por cumplir con la primera condición de la función dada, que indica los valores por la izquierda de 2, es decir, valores menores que 2. , reemplazando. Ahora por la derecha: , por cumplir con la tercera condición de la función dada, que indica los valores por la derecha de 2, es decir, valores mayores que 2. , reemplazando. , por lo tanto: . Sí existe, pues son iguales por izquierda y por derecha. Verificando la última condición: , por lo tanto la función  es continua en .