Introducción
En la actualidad la tecnología evoluciona de manera rápida con más y mejores beneficios para la humanidad. Es allí donde la digitalización cumple una labor representativa, ya que facilita el manejo y el proceso de la información al permitirle a las personas, entre otros aspectos, el mejorar el manejo tecnológico en los procesos cotidianos de en sus diversas actividades.
Por lo anterior, resulta importante comprender los sistemas binarios, sus combinaciones y aplicaciones e implicaciones en el mundo actual, al igual que conocer la infinidad de posibilidades que se habilitan a través de estos sistemas que impulsan el desarrollo de la tecnología, la informática y las comunicaciones. Este último aspecto, es quizá el verdadero alcance de la lógica binario o digital y la representación en estados del mundo análogo.
Objetivos
Objetivo general
Conocer, diferenciar y aplicar los conceptos de análogo, digital, sistemas de numeración, operaciones entre sistemas, álgebra de Boole, funciones y reducción; así como diferenciar cada uno de los tipos o sistemas de numeración digital y los códigos binarios, su representación en funciones y sus diversas formas de reducción, acorde a la digitalización de la información y sus aplicaciones.
Objetivos específicos
- Entender y comprender el concepto y la forma de sistema analógico y sistema digital.
- Conocer y diferenciar los diversos sistemas de numeración y las operaciones que se pueden realizar entre ellos.
- Entender las leyes y teoremas del álgebra de Boole y su aplicación en los sistemas digitales.
- Conocer las características y estructura de las funciones digitales y sus métodos de reducción.
Sistema analógico y sistema digital
El mundo actual también está inmerso en la electrónica y sus desarrollos, en donde las magnitudes analógicas y digitales son las protagonistas. La electrónica analógica se encarga de estudiar las cantidades con valores continuos, más aún si su medida es cuantitativa, permitiendo medir la mayoría de las cosas existentes en la naturaleza, como la temperatura y la presión.
Por su parte, la electrónica digital se centra en las cantidades con valores discretos que permiten representar gran variedad de cosas que pueden ser cuantificadas a saltos y en algunos casos permiten excelentes aproximaciones a las magnitudes analógicas.
"Las magnitudes digitales tienen como ventaja que se pueden almacenar, procesar y transmitir de forma más fácil, eficiente y fiable que los datos analógicos. En algunas oportunidades su almacenamiento y reproducción es más fiel que en los sistemas analógicos" (Floid, 2006).
"Un sistema analógico contiene dispositivos que manipulan cantidades físicas representadas en forma analógica, mientras que un sistema digital es una combinación de dispositivos, diseñada para manipular cantidades físicas o información que estén representados en forma digital" (Floid, 2006).
Características de los sistemas digitales
La electrónica digital utiliza sistemas en los que solo existen dos estados posibles con ondas propias que se representan mediante dos niveles de tensión diferentes: un nivel alto o high y un nivel bajo o low; niveles que pueden representar estados normalmente contrarios como: interruptores abiertos y cerrados, encendido y apagado, lleno y vacío, ceca y lejos, falso y verdadero, entre otros.
Con base en estos dos estados se representan cantidades a través de sistemas de numeración y códigos. La representación numérica de estos dos estados se conoce como binario y los dígitos que se emplean son el uno (1) y el cero (0), que en el sistema binario se les denomina bit y se representan con unos niveles lógicos.
Operaciones lógicas básicas
En su forma más simple, la lógica es la parte del razonamiento humano que indica que una determinada proposición, ya sea una frase o sentencia de asignación, es cierta si se cumplen ciertas condiciones. Las proposiciones pueden ser clasificadas como verdaderas o falsas y son empleadas con frecuencia en la cotidianidad.
El término lógico se aplica a los circuitos digitales y dentro de éstos hay tres operaciones, denominadas operaciones lógicas básicas, que se representan por símbolos, con unas líneas llamadas entradas o imputs y otras conocidas como outputs o salidas.
Las entradas están a la izquierda del símbolo y las salidas a la derecha de estos circuitos, que realizan una operación lógica básica o compuertas lógicas. Es necesario tener presente que cuando un valor lógico registra alto se considerara verdadero y un nivel lógico bajo será considerado como falso.
Sistemas de numeración y operaciones
Un sistema de numeración es un conjunto ordenado de símbolos llamados dígitos que con leyes definidas para la suma, la resta y la multiplicación permiten representar cualquier cantidad o variable de forma cuantitativa.
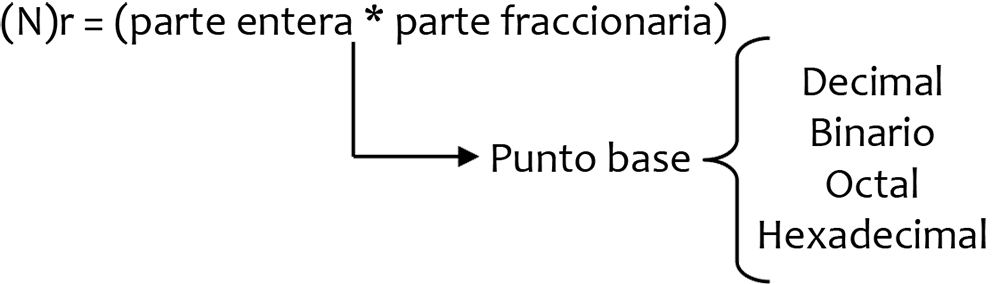
Donde N=número y r= base del sistema.
A continuación se profundiza en cada punto base:
Sistemas de numeración y operaciones
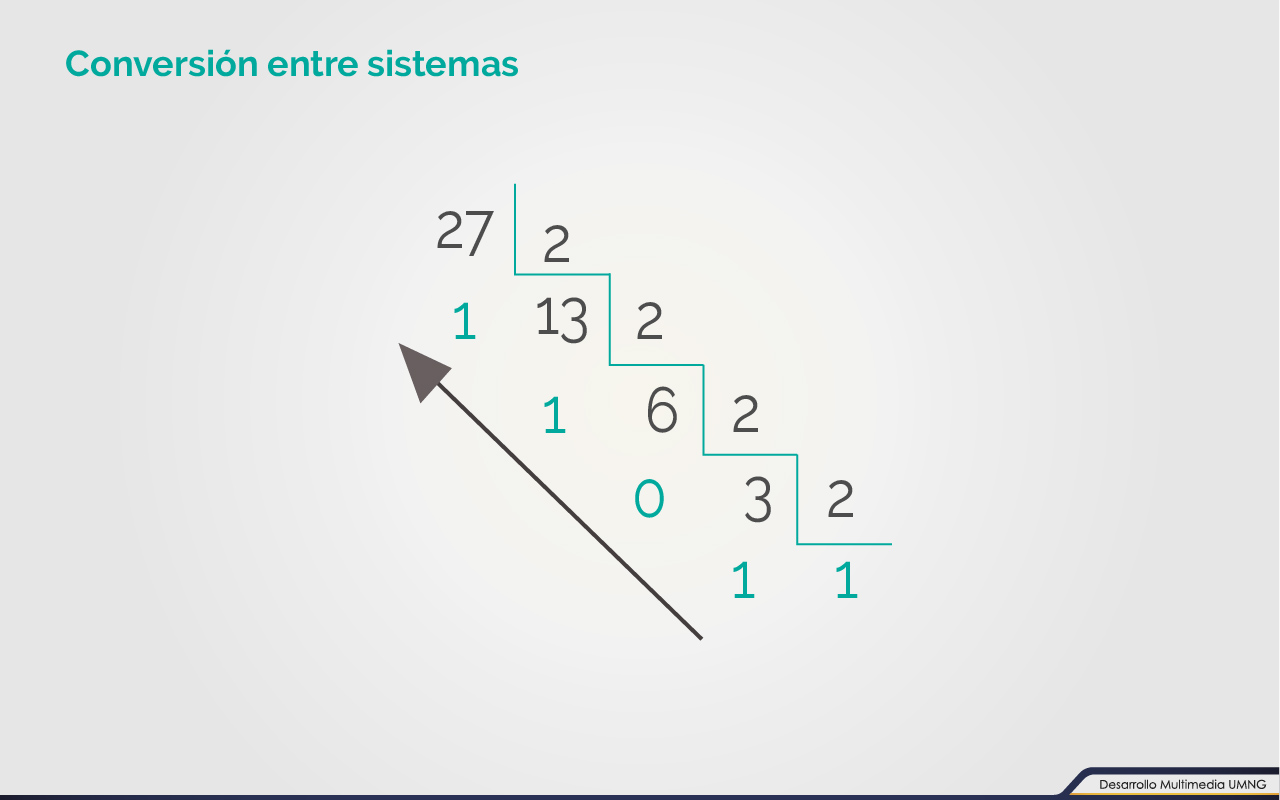
Conversión entre sistemas
- Conversión de decimal a binario
- Conversión de decimal a octal
- Conversión de decimal a hexadecimal
- Conversión de binario a decimal
- Conversión de binario a hexadecimal
- Conversión de binario a octal
- Conversión de octal a decimal
- Conversión de octal a binario
- Conversión de octal a hexadecimal
- Conversión de hexadecimal a decimal
- Conversión de hexadecimal a binario
- Conversión de hexadecimal a octal
La conversión entre diversos sistemas de numeración es de gran utilidad en ingeniería y en sistemas de computación ya que permite pasar datos de un sistema a otro, según se requiera, pero siempre buscando obtener acceso a la información para poder manipular, procesar y almacenar según sea necesario en cada caso.
Operaciones entre los sistemas
Las principales operaciones con números son de tipo aritmético o de tipo lógico y las más comunes entre los diversos sistemas de numeración son suma, resta, producto y complemento.
Con todas las anteriores se puede representar cualquier operación que requiera un sistema de cómputo, a través de las variaciones y combinaciones de las operaciones básicas.
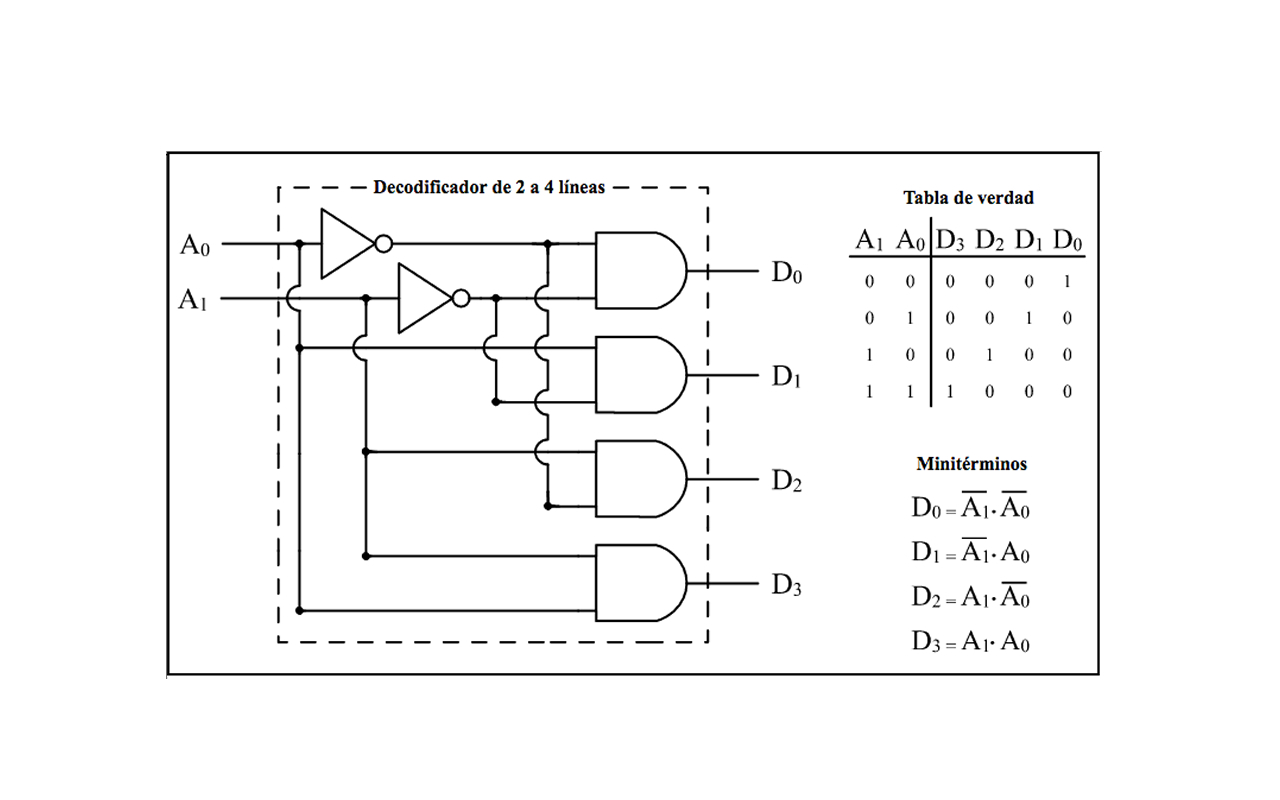
Codificación y/o codificadores
Al grupo de dígitos que constituyen una información específica se le conoce como código y al orden de dicha información se le define como codificar.
En el ambiente de los circuitos digitales existe una variedad de códigos entre los que se encuentran:
Leyes del álgebra de Boole
Las leyes del álgebra de Boole son los postulados básicos sobre los que se fundamenta el análisis lógico y digital. Está conformado principalmente de variables o letras a las que se les asigna un valor lógico, unos complementos como el inverso de una variable y los literales que son variables expresadas en oraciones, funciones o procesos.
Dentro de los procesos del algebra están los elementos básicos de la suma y el producto como elementos primordiales de representación.
Estas leyes se clasifican en dos grandes grupos:
Funciones del álgebra de Boole
El álgebra de Boole permite representar funciones lógicas o circuitales, bajo el proceso de representación de términos, los cuales son el equivalente binario de una representación que utiliza variables para indicar tanto entradas como salidas al sistema o circuito y depende del tipo de arreglo a considerar.
Métodos de reducción
La reducción de funciones digitales permite disminuir el costo de implementación de circuitos y facilita el proceso para los diseñadores.
Los dos métodos principales son:
Resumen
Los sistemas digitales y la numeración utilizada por las computadoras y máquinas electrónicas, que son de uso cotidiano en todos los ámbitos, basan su funcionamiento en los principios básicos de los sistemas digitales y sus parámetros de escritura como funciones lógicas Esto permite realizar diversas operaciones matemático lógicas que agrupan cada día más elementos que permiten realizar tareas más complejas y entender los sistemas digitales, sus conversiones, características y formas de presentación de las señales y variables con respecto a la relación de la vida diaria, pasada o trasladada en forma digital. Para esto último se hace uso de los sistemas de digitalización, acorde al grado de precisión que se requiere en la representación.
El álgebra de Boole es una herramienta fundamental en los sistemas digitales, ya que permite expresar matemáticamente todas las opciones que puede tomar una variable y la forma como cada opción representa una característica del sistema que es irrepetible.
La reducción de funciones es una de las formas primordiales para la implementación de circuitos digitales; una vez planteado el problema a solucionar y seleccionadas las variables del problema se puede extraer la tabla de verdad de la solución y plantear tanto la ecuación como su reducción y la solución más óptima del sistema.
Así mismo, la reducción de funciones se puede realizar con el empleo de los postulados o leyes del álgebra de Boole o a través de los mapas de Karnaugh, siempre y cuando se tengan hasta cinco variables en forma manual o con el apoyo de los sistemas de cómputo cuando se presentan más de cinco variables en la tabla o ecuación.
Bibliografía ()
- Cekit S.A. (1994) “Curso Práctico de Electrónica Digital”. Pereira.
- Dempsey John A., (1996). “Electrónica digital básica: con aplicaciones de circuitos MSI”. Editorial Alfaomega.
- Floyd Thomas L. (2006). Fundamentos de sistemas digitales. Madrid: Prentice-Hall, 2006. 9a ed.
- Mandado Pérez E y Mandado Rodríguez Y. (2008). Sistemas electrónicos digitales. 9a ed. México: Alfaomega.
- Marcus, M. P. (1982)"Circuitos digitales para Ingeniería". Prentice-Hall.
- Morris Mano M. (2002). Digital design. New Jersey: Prentice Hall,. 3a ed. New Jersey: Prentice Hall, 2002.
- Ruiz, Jairo. (1997). "Cartilla de guías para el laboratorio de Circuitos digitales". Bogotá.
- Ruiz, Jairo. (2003) “Elementos de Lógica Digital". U.D. Bogotá.