En algunas ocasiones resulta difícil resolver los problemas de valor inicial en las ecuaciones diferenciales debido a lo difícil que es resolver dichas ecuaciones, y es por esta razón que existen algunos métodos para aproximar soluciones en este tipo de problemas.

En esta unidad se expondrán algunos métodos que permiten solucionar, al menos de manera aproximada, este tipo de problemas. De igual manera se usarán herramientas que facilitarán el entendimiento de los conceptos a trabajar.

Propósito general

Reconocer métodos de aproximación a la solución de ecuaciones y ecuaciones diferenciales.

Propósitos específicos

• Seleccionar el método más apropiado para encontrar soluciones aproximadas en problemas de valor inicial.
• Comprender los diferentes métodos para aproximarse a la solución de ecuaciones diferenciales.
• Resolver ecuaciones diferenciales aplicando un método iterativo.

En esta unidad se explicará la forma de resolver ecuaciones diferenciales ordinarias (EDO) de la forma:

En tal sentido, los métodos de Runge-Kutta permiten estimar algún valor y_i+1 a partir de otro valor y_i, una pendiente m estimada a partir de la función y una distancia h (también llamada paso del método).

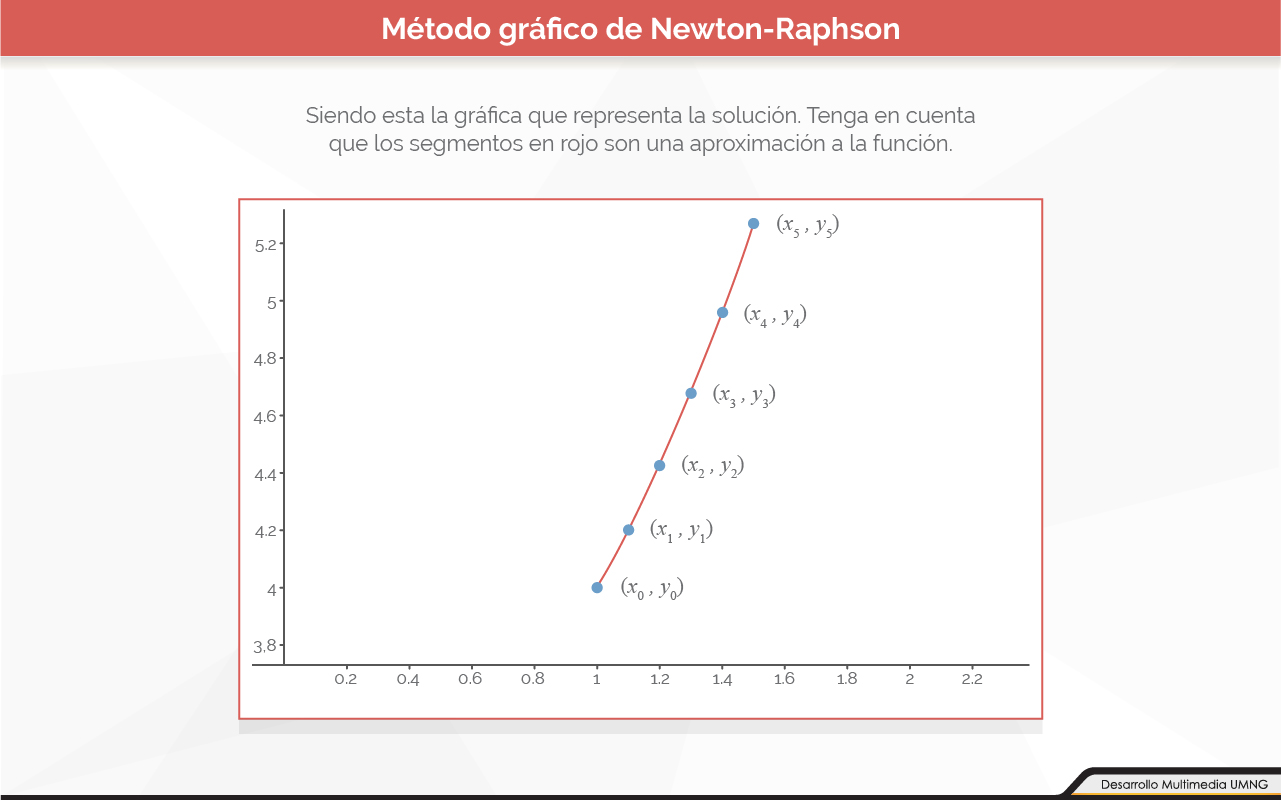
El método de Euler, también conocido como método de tangentes, se caracteriza por ser el primer y más sencillo método para solucionar problemas de valor inicial (PVI) en EDO.

Existen otros métodos que permiten llegar a una solución más aproximada usando una menor cantidad de cálculos. Uno de estos métodos es el de Euler mejorado que además permite aumentar fácilmente la exactitud del proceso.

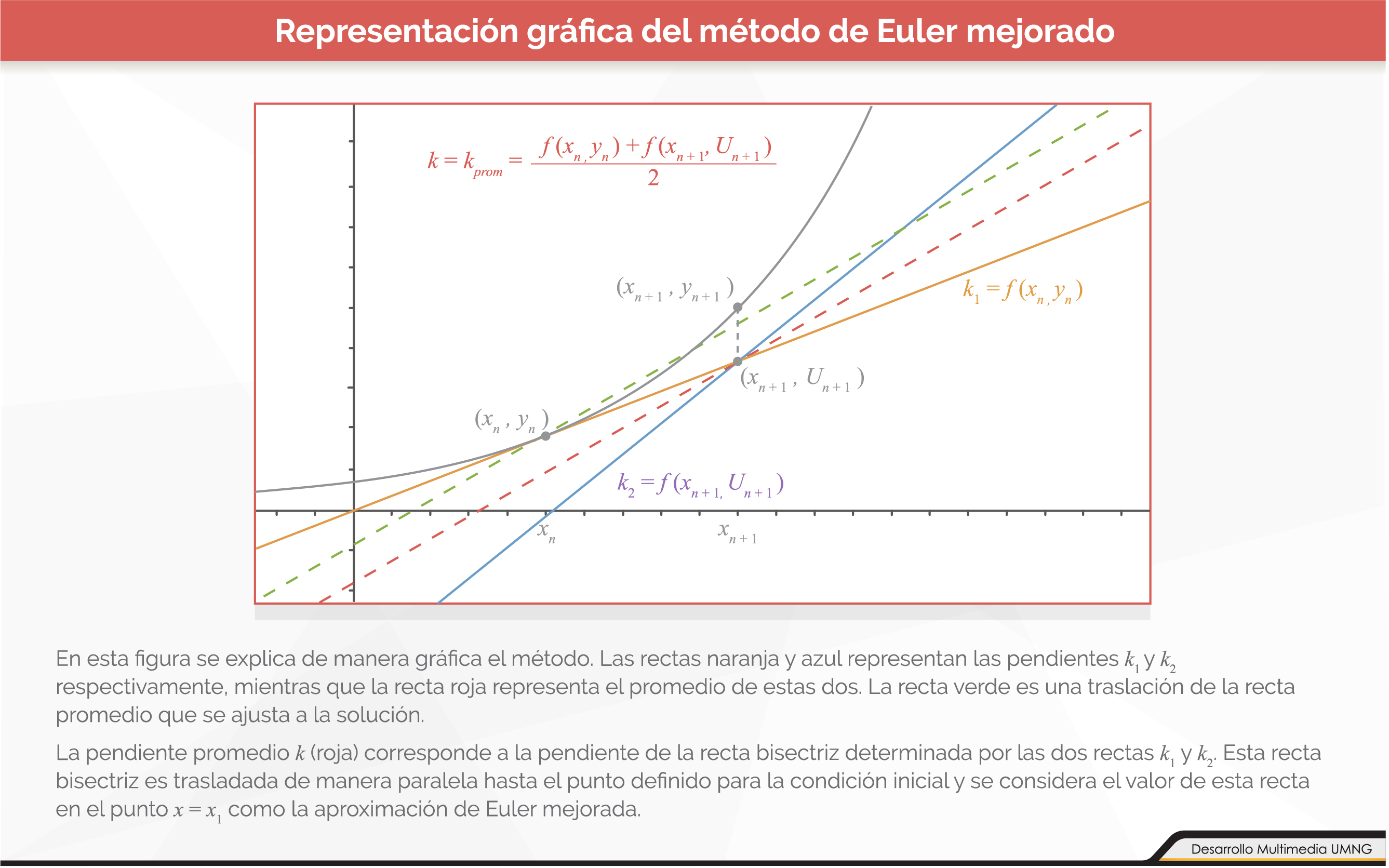
El método de Euler mejorado consiste en tomar las fórmulas del método de Euler para calcular la pendiente en un punto inicial y en un punto final y luego promediarlas. De esta manera el resultado será mucho más acertado a lo largo de todo el intervalo.

El método de Euler mejorado hace parte de una clase general de métodos conocidos como métodos predictores-correctores, en los que primero se calcula una predicción U_n+1 del siguiente valor de y, y posteriormente se utiliza para corregirse a sí misma.

Haga clic sobre el enlace para ver un ejemplo de aplicación del método de Euler mejorado.

Al igual que los métodos expuestos anteriormente, el método RK4 es empleado para resolver EDO de la forma:

Con un valor inicial y(x₀)=y₀ y un paso h también definido por una partición equiespaciada.

Consulte el esquema interactivo para acceder a una actividad de aprendizaje que le permitirá poner a prueba los conocimientos adquiridos hasta este punto.

Material de apoyo

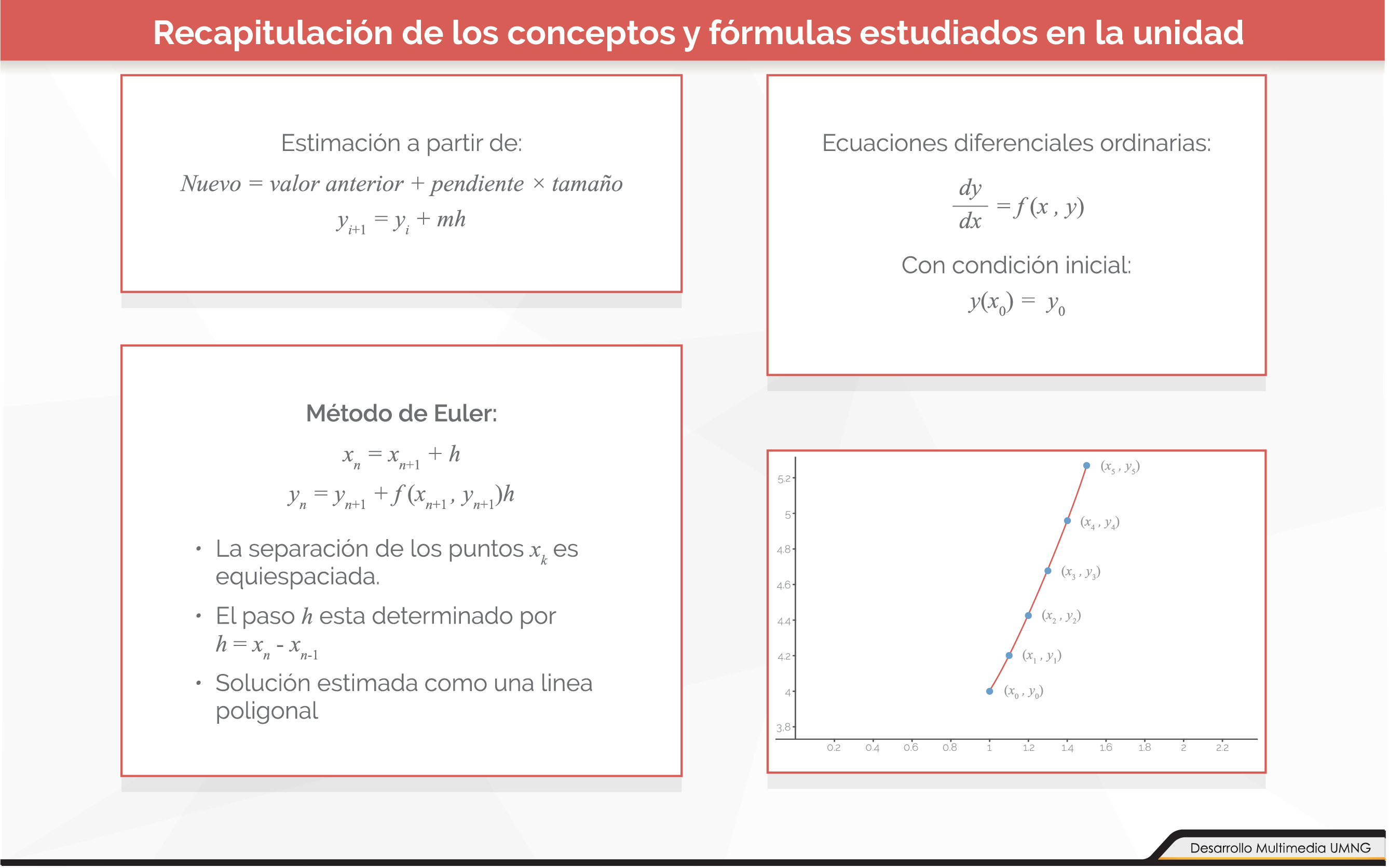
En esta unidad se ofreció un acercamiento a algunas de las maneras de resolver ecuaciones diferenciales a partir de los métodos numéricos más conocidos. Para tal fin los métodos estudiados fueron el método de Euler, el método de Euler mejorado y el método de Runge-Kutta 4 (RK4).

Estos métodos funcionan a partir de un paso determinado h en un intervalo [a, b], partiendo de una condición inicial y(x₀)=y₀. Es a partir de estos elementos que se pueden establecer, de una manera reiterativa, las soluciones aproximadas de la ecuación diferencial. Es importante resaltar que estos métodos no pretenden encontrar la forma concreta de la función que da solución a la ecuación diferencial, sino sus valores ya que estos son los que realmente importan.

En la primera parte de la unidad se analizó el método de Euler y a partir de las fórmulas obtenidas en este, se construyó el método de Euler mejorado. Posteriormente se presentó el método RK4, el cual es el más conocido para resolver ecuaciones diferenciales de manera numérica. En la explicación de este último método se presentó un aplicativo desarrollado en Geogebra para permitirle a los estudiantes tener una mayor apropiación del método.