Introducción
La integral definida es una herramienta de gran versatilidad y aplicabilidad en diferentes campos. Los padres de la administración se valieron de ella para determinar el superávit del consumidor y del productor, entre otras aplicaciones.
El superavit de consumidores y productores en donde se determina el precio de venta de un productos dentro del mercado, es una de las aplicaciones que aporta la integral definida. En estudios anteriores, se aprendió que el punto de intersección de la curva de la demanda y la de oferta para un producto es el precio de equilibrio; en este precio, los consumidores comprarán la misma cantidad del producto fabricado para vender. Algunos consumidores aceptarían gastar más en un artículo que el valor del precio de equilibrio.
La diferencia entre el precio de equilibrio del artículo y los mayores precios que todas esas personas aceptan pagar, se considera como un ahorro de esas personas y se llama el superávit del consumidor.
Observe en la gráfica de la pantalla: el área bajo la curva de demanda es la cantidad total que los consumidores están dispuestos a pagar por q0 artículos. El área sombreada bajo la recta =p0 muestra la cantidad total que los consumidores realmente gastarán en el preciop0 de equilibrio. El área entre la curva y la recta representa el superávit de los consumidores.
Con la gráfica anterior, se da la bienvenida a la integral definida. Dentro de la unidad, también se presentan temas relevantes como el cálculo de áreas, las integrales impropias y las integrales múltiples.
Objetivos
Objetivo general
Calcular áreas bajo la curva de una función, utilizando los métodos de límites, dando una interpretación desde la economía y la administración; así como evaluar probabilidades con funciones conjuntas de densidad y probabilidad.
Objetivos específicos
- Definir ejemplos que relacionen la existencia entre la integral y las áreas definidas.
- Aplicar la integral definida en la solución de problemas donde intervengan como variables de integración los costos y las tasas.
- Plantear problemas que relacionen el cálculo integral y la teoría de la probabilidad.
Integral definida
La integral definida es el área fundamentada en una infinita sumatoria de rectángulos, donde la base de cada uno tiende a cero y está delimitada por dos parámetros sobre el eje x.
En la figura, los límites o parámetros están en el intervalo (0,2), obsérvese que el cálculo de la integral es el área del triángulo rectángulo que se forma bajo la curva f(x)=y=x.
La solución paso a paso de la integral definida:
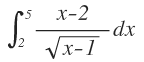
La encuentra aquí y es muy útil para su comprensión.
Revise cuidadosamente los ejemplos que evalúe y desarrolle los ejercicios.
Cálculo de áreas
El cálculo de áreas es una de las aplicaciones más vistas de la integral definida. A continuación, se explica el concepto graficamente:
El área A de la región S que se encuentra debajo de la gráfica de la función F(x) es el límite de la suma de las áreas de los rectángulos A.
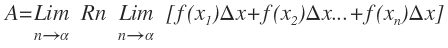
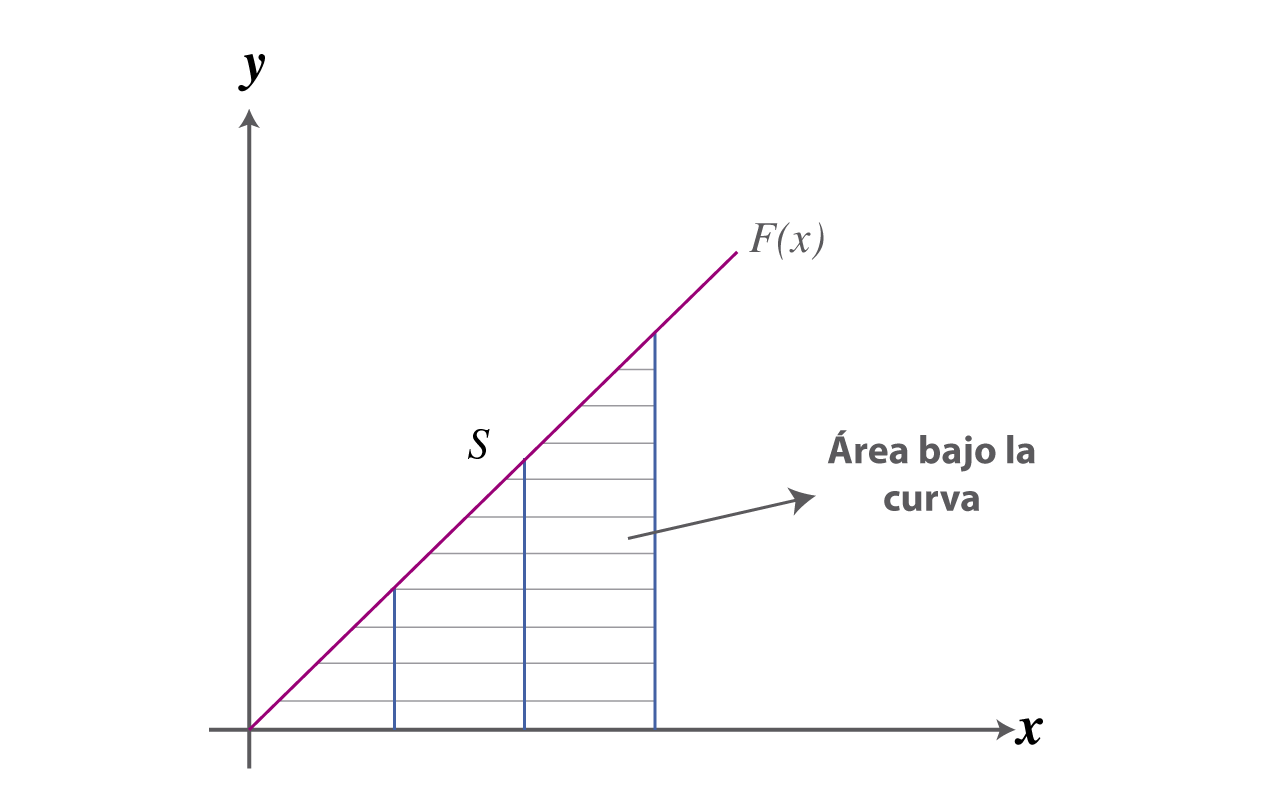
Para hallar el área bajo la curva de una función que corresponde a una figura geométrica no definida, hay que determinar los límites integración o puntos que corresponden a los extremos de las áreas a calcular.
Cálculo de áreas
Área encerrada entre dos curvas
El área encerrada entre dos funciones f(x) y g(x), se define como la resta entre el área de la función superior menos el área de la función inferior.
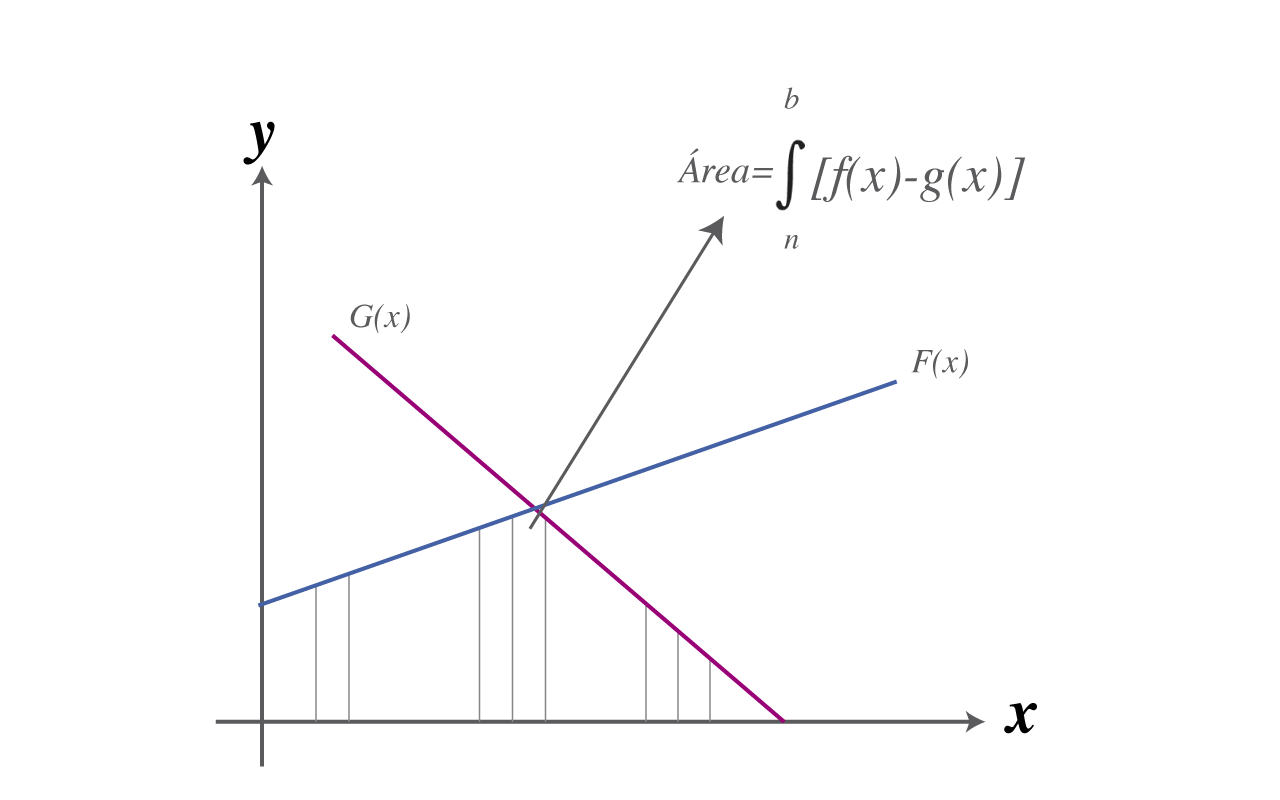
El cálculo de áreas se realiza mediante la determinación del área bajo la curva superior f(x) menos el área bajo la curva inferior g(x).
Para reconocer que la integral es el área bajo una curva se va a verificar que ∫03 xdx=9/2, es la misma que el área del triángulo rectángulo base y altura 3, siga cada uno de los pasos del proceso que se muestra aquí.
Área de la región entre dos curvas
Con pequeñas modificaciones, se puede extender la aplicación de la integral definida para cubrir no solamente el área de la región bajo una curva, sino el de una región comprendida entre dos curvas.
Integrales impropias
La definición de la integral definida requiere que el intervalo [a,b] sea infinito. El teorema fundamental del cálculo con el que se han estado evaluando las integrales, exige que f(x) sea continua en [a,b]. En esta sección, se estudian las integrales impropias; las cuales incumplen estas características bien sea porque:
- Uno o ambos límites de integración son infinitos.
- En un número finito de esos dos supuestos se llaman integrales impropias.
- Si f es continua en el intervalo [a,b] , excepto en un c de [a,b] en el que f tiene una discontinuidad infinita entonces:
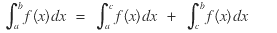
En cada caso, si el límite existe, se dice que la integral impropia converge; si no existe el límite se dice que la integral impropia diverge. En el tercer caso, la integral impropia de la izquierda diverge si alguna o ambas de las dos integrales impropias de la derecha divergen.
Dé click aquí y observe los ejemplos de integrales impropias y luego resuelva los ejercicios.
Integrales múltiples
La integral múltiple es una extensión de la integral sencilla que se ha visto hasta el momento. Con la integral múltiple, se puede determinar volúmenes (caso de 3 variables).
Una integral múltiple está definida por dos o más funciones de variables x, y, z, etc., al mismo tiempo. Por ejemplo, se podría calcular la integral de la función:
g(x,y)= g´(x,y)dxdy
Tiene sentido diferenciar una función de varias variables respecto a una de ellas, manteniendo constantes las demás. Por ejemplo, si se da la derivada parcial:
fx(x,y) = 2xy
Considerando a y como constante, se integra con respecto a x, obteniendo así:

Nótese, que la "constante" de integración C(y), es una función de y. En otras palabras, integrando respecto de x sólo se es capaz de reconstruir fx(x,y) parcialmente. En adelante, el módulo es dedicado a extender la integración definida a funciones de varias variables. En este ejemplo, considerando y constante, se puede aplicar el teorema fundamental del cálculo para evaluar.
Observe los siguientes ejemplos de integrales múltiples y desarrolle los ejercicios que se encuentran al final del documento.
Resumen
La integral definida como tema de estudio en las matemáticas, es una herramienta de gran versatilidad y aplicabilidad en diferentes campos.
Una de las aplicaciones más vistas de la integral definida es el cálculo de áreas. Para hallar el área bajo la curva de una función que corresponde a una figura geométrica no definida, hay que determinar los límites de integración o puntos que corresponden a los extremos de las áreas a calcular.
Por lo anterior, en la unidad se presentaron temas significativos como: la integral definida; el cálculo de áreas que se realiza mediante la determinación del área bajo la curva superior f(x) menos el área bajo la curva inferior g(x).
Se hizo énfasis también, en el área encerrada entre dos curvas; las integrales impropias y las integrales múltiples.
Bibliografía ()
Referencias Web
- Haeussler, F., y Jr., E. (2003). Matemáticas para administración y economía. (P. Educación, Ed.) Recuperado el 19 de marzo de 2015, de Academia.edu: http://www.academia.edu/4960239/Esta_d%C3%A9cima_edici%C3%B3n_de_Matem%C3%A1ticas_para_Administraci%C3%B3n_y_Econom%C3%ADa



