En la vida diaria ocurren diversos fenómenos de orden económico, social, político, educativo, biológico, entre otros, los cuales aparecen, se transforman y desaparecen. Frente a tan abundante y complejo material es preciso tener un registro ordenado y continuo, a fin usar los datos necesarios para el estudio de lo que ha sucedido, sucede y sucederá. Esta labor predictiva requiere un método (conjunto de reglas y principios) que propicien el adecuado ordenamiento, la cuantificación y el análisis de dichos fenómenos, método denominado como estadística.

Debido al avance tecnológico y el crecimiento de las empresas modernas, es imperativo el uso de métodos estadísticos que suministren información de la producción, control de calidad, inspecciones de artículos, entradas y salidas de materias primas, implementación de planes de mejoramiento, etc.

Cuando un artículo debe ser sometido a un control de calidad, son establecidas técnicas de muestreo para reducir el número de elementos defectuosos. Las conclusiones permitirán mejorar la nueva producción. El análisis de datos se realiza mediante técnicas proporcionadas por la estadística, la cual se ha dividido en dos partes:

1. Estadística deductiva o descriptiva: sólo describe una serie de datos, sin llegar a conclusiones ni generalizar respecto al grupo más grande o población.
2. La otra analiza y trata de establecer conclusiones acerca de un grupo mayor, basado en la información de un grupo menor o muestra.

El análisis estadístico usa diversos términos corrientes, necesarios e imprescindibles para la comprensión de temas posteriores. En todo estudio estadístico el investigador está interesado en una colección o conjunto de observaciones específica, denominada población o universo.

Objetivo general

Resumir y describir adecuadamente conjuntos de datos por medio de métodos gráficos y medidas numéricas.

Objetivos específicos

• Definir los conceptos básicos de la estadística descriptiva.
• Aplicar las técnicas que permitan la elaboración de tablas o cuadros que visualicen la información suministrada en un ejercicio.
• Describir la información suministrada por gráficos estadísticos, interpretando con ayuda de medidas de tendencia central, dispersión y definir con criterios sus conclusiones estadísticas.

Existen ciertos elementos básicos para iniciar el estudio de la estadística, pilar de los demás que veremos durante la ruta de estudio, razón por la que es importante conocerlos e identificarlos en cualquier ejercicio posterior, pues permiten identificar las características de un hecho a analizar, los demás conceptos de la estadística surgirán como derivados de estos:

• Estadística: es la “Ciencia del Estado”, puesto que desde la antigüedad los Estados han recogido datos sobre sus habitantes con diversos objetivos (recaudar impuestos o reclutar jóvenes para el ejército). También puede significar la colección de datos. Muchas lenguas usan misma palabra para referirse la ciencia que estudia y designa los datos.
• Estadística descriptiva: muestra, representa y resume situaciones prácticas en las que existe incertidumbre, las cuales afectan colectivos con un número importante de individuos (personas, objetos producidos industrialmente o resultados de una cosecha).
• Estadística inferencial: busca el conocimiento de la población a partir de observaciones relativas a sólo una parte de ella, conocida como muestra.

A medida que avanzan los tiempos y la modernidad se apropia del mundo es más compleja la toma de decisiones acertadas en el ámbito empresarial, por lo que es necesario implementar métodos de investigación cualificados. Las investigaciones con base en el método científico y aquellas basadas en análisis de datos estadísticos proponen una misma solución a problemas.

La recopilación de datos es el primer paso del proceso, en el que hay que considerar el método y características del muestro. Cuando se reúnen todos los datos a estudiar se denomina censo; cuando se analiza una parte de ellos, encuesta.

La estadística descriptiva se refiere al conjunto de datos con un papel decisivo para desarrollar una investigación, mediante una clasificación que permita hallar sus características de manera objetiva y eficiente. Investiga los métodos y procedimientos; además, establece reglas para manejar los datos, de modo que la información entregada sea lo más confiable posible, para expresar comparaciones de forma precisa.

El dato es un material indispensable que debe ser procesado, de manera que su recopilación y posterior análisis ayude en la proposición de soluciones a los problemas del entorno laboral.

Recolectar los datos demanda organizarlos de forma ordenada y sistemática para luego analizarlos. La tabla es la mejor y más frecuente forma de hacerlo. En los negocios es común el estudio de patrones entre dos o más variables categóricas. Una tabla de clasificación cruzada o de contingencia presenta la variación de los elementos en relación a otros, razón por la que también son conocidos como gráficas para datos bivariados.

La frecuencia es el número de veces que se repite un dato, los cuales son registrados y organizados en tablas. Cuando los datos estadísticos son demasiados, deben ser organizados y clasificados de manera diferente para iniciar su análisis, mediante métodos estadísticos que estudian su comportamiento y variabilidad con relación a ciertas condiciones (ver ejemplo).

Inicialmente los datos son agrupados en distribuciones de frecuencias, que los ordenan por clase, indicando el número que contiene cada clase. Así, maneja los datos como un carácter de conjunto (renunciando a su carácter individual), elemento clave en la estadística. Los métodos gráficos para presentar la información significan un elemento clave dentro de este proceso, en razón a que propician un adecuado entendimiento de los datos recopilados y la información que se puede extraer de éstos, entre los que se destacan: el histograma, las ojivas o polígono porcentual acumulado, los diagramas de puntos y líneas, el pictograma, el polígono de frecuencias, los diagramas circulares, los diagramas de barras y el cartograma.

También hay que considerar estos elementos fundamentales:

• Rango: diferencia entre los valores extremos de los intervalos (el mayor y el menor de todos), rango en el que están distribuidos los demás valores del conjunto, por lo que también se le llama recorrido.
• Número de intervalos de clase: subconjuntos de medidas o datos. Tienen un límite inferior (dato menor) y un límite superior (dato mayor).

Hasta el momento nuestro estudio ha estado centrado en las técnicas y los métodos utilizados para la ordenación, agrupación, organización y presentación de datos recolectados, así como su interpretación inicial y básica, incluyendo su representación gráfica como herramienta para la toma de decisiones empresariales.

Ahora veremos una serie de métodos que amplían los análisis obtenidos, los cuales pueden ser respecto a la población (parámetros) o la muestra (estadígrafos). Dichos métodos están agrupados en varias categorías, entre las cuales abordaremos las de tendencia central.

Las medidas de tendencia central describen y unifican mediante un promedio o número único, el cual se trata de localizar en la mitad de la serie (posición de un valor en la variable a estudiar), de forma que represente todo el conjunto de las observaciones.

Es una medida que va a distinguir a la población o la muestra en estudio, fundamemntada en tres conceptos: media aritmética, moda y mediana.

Las medidas de tendencia central muestran el comportamiento de datos en forma de claras características comunes en determinados subgrupos de elementos o datos en cuanto a su frecuencia y a los datos alrededor o en la vecindad de estos haciendo que la grafica curva de estos datos se convierta en una campana. Por lo general la mayor densidad de frecuencia esta en las partes centrales de las graficas de aquí se deriva el nombre de medidas de tendencia central y son la media aritmética, la moda y la mediana.

Existen otras medidas de posición como los deciles, cuartiles, percentiles, el promedio ponderado y las otras clases de media diferentes a la aritmética, las cuales describen con mayor detalle el comportamiento de los datos. Estas medidas dividen un conjunto de datos en grupos con el mismo número de individuos.

El rango es muy influenciable por los valores extremos. Para eliminar esta influencia suele analizarse la situación del intermedio de la distribución, la cual hace referencia al rango intercuartil, diferencia entre el tercer cuartil (Q₃) y el primero (Q₁).

Otras medidas de tendencia central importantes son la media geométricay la media armónica.

Los deciles, cuartiles, percentiles y el promedio ponderado son otras clases de media diferentes a la aritmética, que describen detalladamente el comportamiento de los datos (ver ejemplo).

Estas medidas dividen un conjunto de datos en grupos con el mismo número de individuos. Para una mejor comprensión, vea los ejemplos en el documento que acompaña esta pantalla.

Las medidas de variabilidad absoluta amplían el concepto de variabilidad, como el método de las medias de tendencia central, que describen el comportamiento de los datos en una distribución de frecuencia. Las informaciones que proporcionan estas medidas son limitadas y no dicen nada sobre cómo están distribuidos o dispersos los datos con relación a la tendencia central. Tampoco poco indican sobre un determinado dato con relación a otros de la distribución.

La interpretación de un grupo de datos individuales necesita de informaciones que permitan apreciar la dispersión de los valores alrededor de la medida de tendencia central. Estas medidas son importantes por sus propiedades algebraicas, por lo que es frecuente su implementación en la solución de problemas de estadística aplicada.

En la siguientes pantallas conoceremos en detalle dos conceptos clave:

• Desviación media
• Desviación media absoluta

En toda distribución la suma de las desviaciones de cada valor de la variable respecto a la media es cero. Significa que la suma de las desviaciones 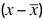de las variables mayores que la media es igual y de signo contrario a la suma de las desviaciones de las variables menores que la media, razón por la que emplea los valores absolutos de las desviaciones para obtener la desviación media.

Para calcular la varianza media es necesario prescindir de los signos negativos y tomar los valores absolutos de las desviaciones respecto a la media aritmética. Si elevamos al cuadrado las desviaciones, logramos que todos los resultados positivos, sumando los cuadrados de las desviaciones y dividiendo por N, resulte el estadístico llamado varianza, base para calcular la desviación estándar.

Las medidas de variabilidad absoluta o de dispersión analizan un grupo de datos de manera más rigurosa y profunda, para extraer información sobre qué tan dispersos resultan los datos alrededor de la media y así verificar su comportamiento (ver ejemplos).

Esta medida de dispersión es considerada como una de las medidas más fácil de calcular, por lo que es utilizada en la mayoría de los casos, con el único fin de agilizar las operaciones, de ahí que el resultado se le considere como una aproximación a la cuantificación de la dispersión. Para ver cómo se escribe la desviación media (representada por DM) de una muestra que contiene n observaciones x1, x 2, xn, haga clic en este link.

El ejemplo que acompaña esta pantalla (parte derecha) puede aclarar cómo obtener la desviación media absoluta. Es clave su lectura para mejorar la experiencia de aprendizaje.

Las medidas de dispersión o variación absoluta se expresan en las mismas unidades en que se ha medido la variable. Si necesita comparar dos o más series de observación, no es posible realizarla si utiliza la dispersión absoluta. En esta medida pueden ocurrir dos casos posibles: que las unidades de medidas sean iguales o diferentes. En el primer caso, las dos series pueden tener medias aritméticas diferentes. Al estar expresadas en las mismas unidades, las desviaciones estándar son comparables pero no aportan una correcta apreciación sobre las series comparadas. En el segundo caso no es posible la comparación por medio de la dispersión absoluta.

Para efectuar comparaciones entre series de observaciones se utiliza la dispersión relativa, que es adimensional.

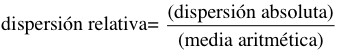
Si la dispersión absoluta es la desviación estándar S. la dispersión relativa recibe el nombre de coeficiente de variación, que permite ver la homogeneidad o la heterogeneidad de la distribución de los datos. A mayor dispersión, mayor heterogeneidad; a menor dispersión, los datos son más homogéneos. La fórmula para encontrar el coeficiente de variación es la desviación estándar o típica dividida entre la media aritmética:

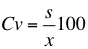
Este coeficiente tiene diversas aplicaciones en cualquier ámbito económico, social, político o ambiental.

Lectura complementaria

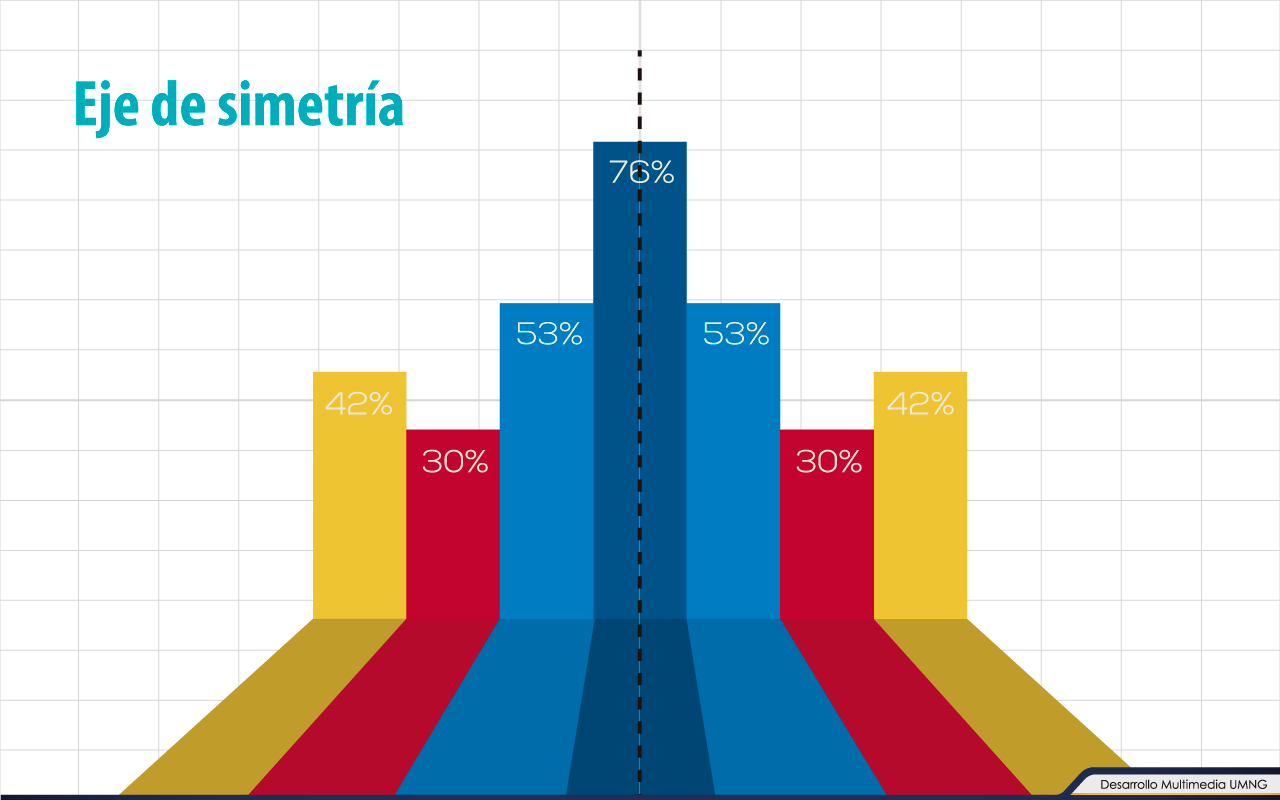
Forma es la apariencia externa de la distribución de frecuencias o de una colección de datos cuantitativos, representada por el aspecto gráfico. Incluye la simetría o asimetría de la curva y el grado de apuntamiento o achatamiento de la curva. Son medidas relativas (cocientes o razones) y no están expresadas en ninguna unidad de medida. Una distribución es simétrica cuando la curva que representa la distribución de datos es exactamente igual a ambos lados de un punto de referencia.

Karl Pearson investigó los coeficientes de asimetría. A él se debe la relación empírica que en las distribuciones moderadamente asimétricas la mediana está aproximadamente a 2/3 partes de la distancia de la moda a la media. El coeficiente de asimetría de Pearson depende de la media y la mediana. Si es mayor que cero, se llama asimetría positiva; caso contrario, es asimetría negativa; si es cero, la distribución es simétrica:

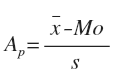
La medida de Bowley depende de los cuartiles. Se refiere la posición de los cuartiles Q₁ y Q₃ con relación a la mediana (Q₂), para determinar la simetría de la distribución:

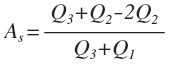
Se refiere la posición de los cuartiles Q₁ y Q₃ con relación a la mediana (Q₂), para determinar la simetría de la distribución.

Las curvas de distribución, comparadas con la curva de distribución normal, pueden presentar diversos grados de apuntamiento o de altura en la cima de la curva, lo que se conoce como curtosis o apuntamiento. La siguiente es la fórmula para calcularla:

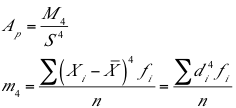
El valor de A_p en la curva normal es 3.

Según su apuntamiento, de acuerdo con el grado de concentración que representan los valores en la región central de una distribución, reciben nombres como:

• Mesocúrtica: la curva tiene una concentración normal.
• Leptocúrtica o apuntada: en la que existe gran concentración. Es la de mayor apuntamiento.
• Platicúrtica: la de menor apuntamiento, debido a la baja concentración.

La estadística descriptiva es usada para explicar, detallar y resumir conjuntos de datos o variables definidas teóricamente. Para lograr el objetivo usa tablas de frecuencias, medidas de tendencia central, medidas de localización, medidas de dispersión y gráficos estadísticos.

Las medidas de tendencia central resumen la magnitud de un conjunto de datos en un valor, en torno al cual se agrupan (centro que puede estar definido de varias maneras). Principalmente, aunque se han definido otras, se usan la media, la mediana y la moda.

Las medidas de dispersión describen qué tan agrupados o separados están los datos alrededor de los valores de tendencia central. Aunque existen medidas de dispersión definidas en torno a la mediana, generalmente se definen al comparar los datos con la media. Las medidas más usadas son la varianza, la desviación estándar y el coeficiente de variación; también son conocidas la desviación media y el rango.

Los sistemas o métodos estadísticos sirven para propósitos descriptivos, organizar y resumir datos numéricos, campos de estudio de la estadística descriptiva. Su aplicación está en diversas áreas, como mercadotecnia, contabilidad, control de calidad, estudios de consumidores, análisis de resultados deportivos, administradores de instituciones, educación, organismos políticos, médicos, entre otros.

La estadística descriptiva es una disciplina que proporciona un conjunto de métodos y procedimientos para recopilar información, clasificar, encontrar las características de los datos y hacer una buena interpretación de los mismos; así, es posible emitir una conclusión acertada respecto a un tema de interés.