Introducción
Como se mencionó en la unidad uno, las nociones de población y muestra son parte fundamental en cualquier investigación. En esta unidad se estudiarán de manera más amplia, en particular en el contexto del concepto de variables aleatorias, destacando la importancia de conocer la distribución muestral de un estadígrafo, ya que con ésta se puede realizar el proceso de inferencia del parámetro, dado que casi nunca es posible tomar todas las muestras de una población. Al conocer la distribución del estimador, se puede hacer la inferencia del mismo a partir de una sola muestra y, de igual forma, se puede estimar el error para un tamaño de muestra dado.
Objetivos
Objetivo General
Identificar las muestras y los estadísticos que las describen.
Objetivos Específicos
- Manejar el concepto del teorema del límite central.
- Comprender y aplicar las distribuciones muestrales de medias, varianzas y proporciones, y aplicar la distribución normal.
- Realizar estimaciones por intervalos para la media, proporción y para la varianza.
Teorema del límite central
Error muestral
Cuando se calcula un estadístico a partir de una muestra, llámese media, desviación estándar o proporción para estimar parámetros poblacionales, esto siempre conlleva algún error. Por ejemplo, suponga que en un grupo de estadística se tienen 40 estudiantes (población) y se promedia su estatura obteniéndose µ=1,68 m (parámetro poblacional). Si se elige una muestra aleatoria de 15 estudiantes y se calcula la media muestral de estaturas obteniéndose (estadístico), se observa que existe una diferencia entre el parámetro y el estadístico que se denomina error muestral.
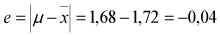
Consulte un ejemplo de errores muestrales.
Distribución muestral de medias
Hay que recordar que en la distribución normal, la variable estandarizada permitía calcular la probabilidad de un evento, dada una variable aleatoria mediante:

Cuando se extraen muestras de tamaño mayor a 30 o bien de cualquier tamaño de una población normal, la distribución muestral de medias tiene un comportamiento aproximadamente normal, por lo que se puede utilizar la fórmula de la distribución normal con 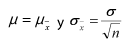 y , entonces la fórmula para calcular la probabilidad del comportamiento del estadístico, en este caso la media de la muestra, se puede observar al hacer clic aquí.
y , entonces la fórmula para calcular la probabilidad del comportamiento del estadístico, en este caso la media de la muestra, se puede observar al hacer clic aquí.
Consulte un ejemplo de distribución de medias muestrales.
Para ampliar la información sobre este tema, consulte también en qué consiste la distribución muestral para la diferencia de promedios y el siguiente ejemplo.
Distribución muestral de la varianza
Si se extrae una muestra aleatoria de tamaño n de una población normal con media µ yvarianzaσ2, y se calcula la varianza muestral, se obtiene el valor del estadístico s2 que se utilizará para conocer la σ2, mediante una variable aleatoria chi cuadrada con “n-1” grados de libertad. Formalizando con el siguiente teorema: sis2es la varianza de una muestra aleatoria de tamaño “n” que se toma de una población normal que tiene varianzaσ2, entonces el estadístico:
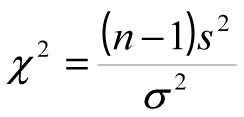
Tiene una distribución chi cuadrado con v=n -1, grados de libertad.
Consulte un ejemplo de distribución de varianzas muestrales.
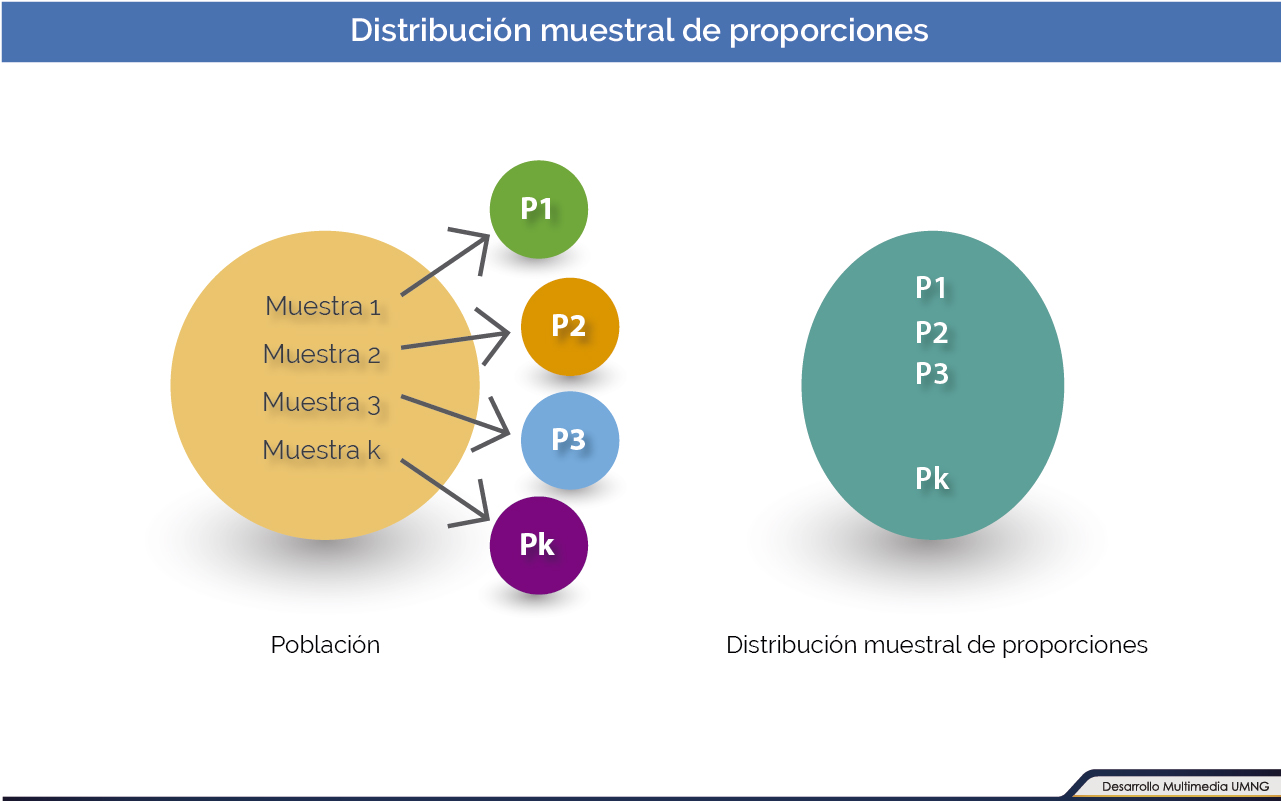
Distribución muestral de las proporciones
Cuando se requiere investigar la proporción de algún atributo en una muestra (variables cualitativas), la distribución muestral de proporciones es la adecuada para dar respuesta a dichas situaciones. Esta distribución se genera de igual manera que la distribución muestral de medias, a excepción de que al extraer las muestras de la población, se calcula el estadístico proporción (p=x/n en donde "x" es el número de éxitos u observaciones de interés y "n" el tamaño de la muestra), en lugar del estadístico promedio. La fórmula que se utilizará para el cálculo de probabilidad en una distribución muestral de proporciones, está basada en la aproximación de la distribución normal a la binomial. Esta fórmula servirá para calcular la probabilidad del comportamiento de la proporción en la muestra.

Si es una población finita:
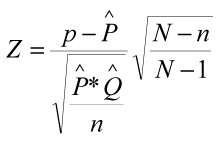
Consulte un ejemplo de distribución de proporciones muestrales
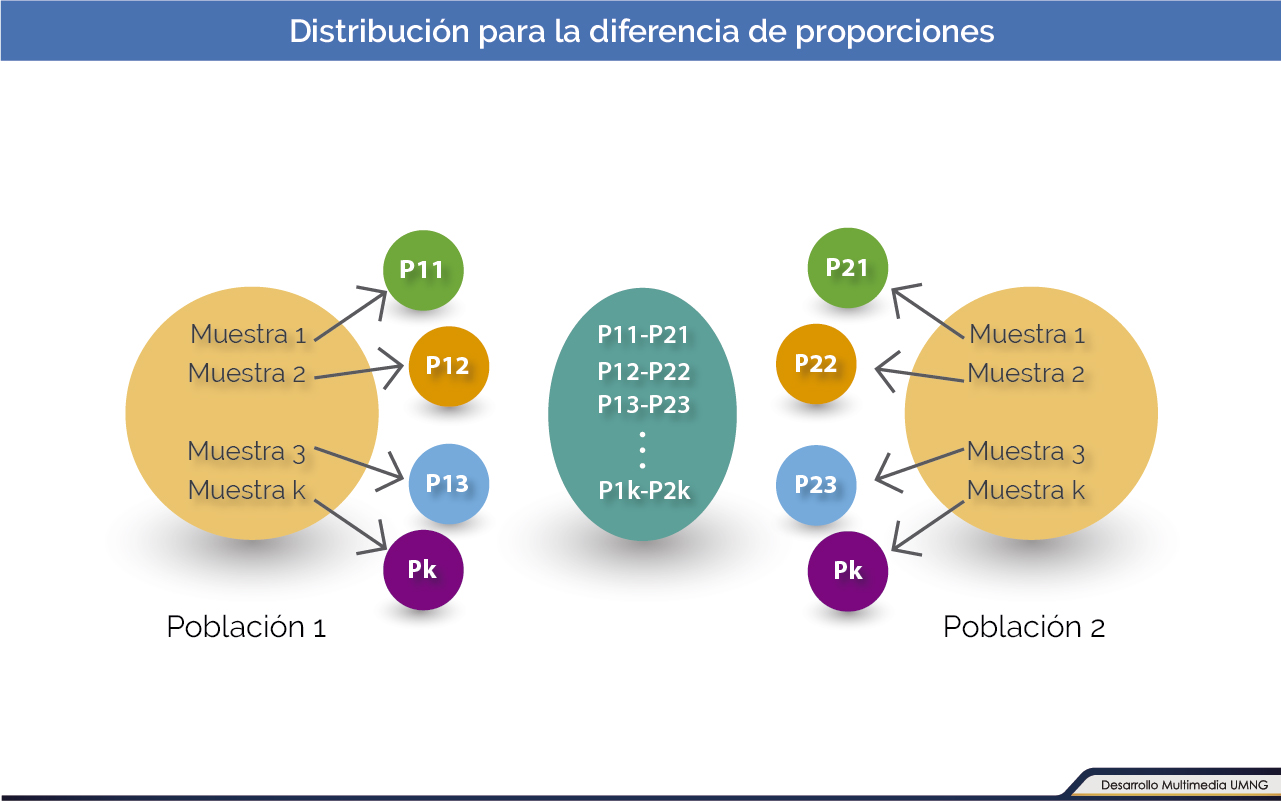
Para profundizar en este tema revise en que consiste la distribución muestral de diferencia de proporciones y un ejemplo de este.
Estimación por intervalos
El principal propósito de la presentación de variables y sus distribuciones muestrales, consiste en realizar conclusiones acerca de los parámetros poblacionales. Por ejemplo, en el teorema del límite central está incluida la media poblacional que si se despeja quedaría en términos de los estadísticos de la muestra. En este aparte se trabajará de manera formal el propósito de la estadística inferencial para una y dos poblaciones.
Para profundizar en este tema consulte los siguientes apartados:
- Intervalo de confianza.
- Estimación de la media para muestras grandes – Ejemplo 1.
- Estimación de la media para muestras pequeñas - Ejemplo 2.
- Estimación de la proporción de una población - Ejemplo 3.
- Estimación de la diferencia entre medias de dos distribuciones normales, varianzas desconocidas pero iguales - Ejemplo 4.
- Estimación de la diferencia entre medias de dos distribuciones normales, varianzas desconocidas y diferentes - Ejemplo 5.
- Estimación por intervalos para observaciones pareadas - Ejemplo 6.
- Estimación por intervalos para la varianza - Ejemplo 7.
Lo invitamos a ver el siguiente video sobre estimación por intervalos.
Resumen
En la presente unidad se describieron las distribuciones muestrales de medias y varianzas en variables cuantitativas, y la distribución muestral de proporciones para variables cualitativas. Con las anteriores bases se realizaron estimaciones por intervalos y su aplicación en ciencias e ingeniería.
Bibliografía ()
- Walpole, R., Myers, R., Myers, S., y Ye, K. (2007). Probabilidad y estadística para ingeniería y ciencias. 8. ª ed. México: Pearson Educación.
Referencias Web
- De la Torre, L. (2003). Curso de estadística I, unidades 1 y 2. Recuperado de: https://goo.gl/ADE6Kq.
- De la Torre, L. (2003). Curso de estadística I, unidad 3. Recuperado de:https://goo.gl/P63qSx
- De la Torre, L. (2003). Teorema del límite central. Recuperado de: https://goo.gl/XatTaE